
乔治·布尔(George Boole)是一位英国数学家,他提出了一套逻辑理论和代数方法,如今这些理论和方法成为包括计算机在内的所有电子设备的基础。他出身卑微,从牛顿、拉普拉斯、拉格朗日等古典数学家那里自学数学。
20岁时,尽管他没有接受过任何正规教育,但他已经开办了自己的第一所学校。他写了几篇关于逻辑理论的文章,并且是第一个将代数符号与可以用逻辑形式和三段论表示的符号进行类比的英国人。
乔治·布尔(1815-1864)自学成才的数学家

乔治·布尔出生在英国林肯郡的一个工人阶级家庭。他的父亲约翰·布尔是一个鞋匠,也是第一个教他数学的人。他的母亲是一位女仆。
乔治·布尔除了上过小学外,没有接受过任何正规教育。相反,他会利用闲暇时间阅读著名数学家的著作,自学古典语言和外语,如拉丁语、法语和希腊语。
到他16岁时,他父亲的生意开始走下坡路。他得帮家里赚钱,所以他决定在当地的小学教书,给学生做家教。他还教拉丁文作为另一种谋生手段。在他20岁的时候,他开办了他的第一所私立学校,以支持当地孩子的教育。他担任了15年的校长,期间一直自学,学习微分方程、变分微积分和其他数学学科。
到1841年,他开始发表有关代数的论文,用符号方法解方程。他把论文提交给了《剑桥数学杂志》。他的《分析变换理论研究》论文主要研究微分方程和线性变换的代数问题,其中他强调不变性的概念。他在《英国皇家学会哲学学报》上发表的论文讨论了如何将代数和微积分结合起来。这为他赢得了皇家学会的第一枚数学金牌。
1847年,他详细描述了逻辑如何与数学而不是哲学更紧密地联系在一起。他逐渐名声大噪,被任命为爱尔兰科克市皇后学院的数学教授。在那里,他遇到了自己的妻子玛丽·埃佛勒斯(也是一位数学家)。
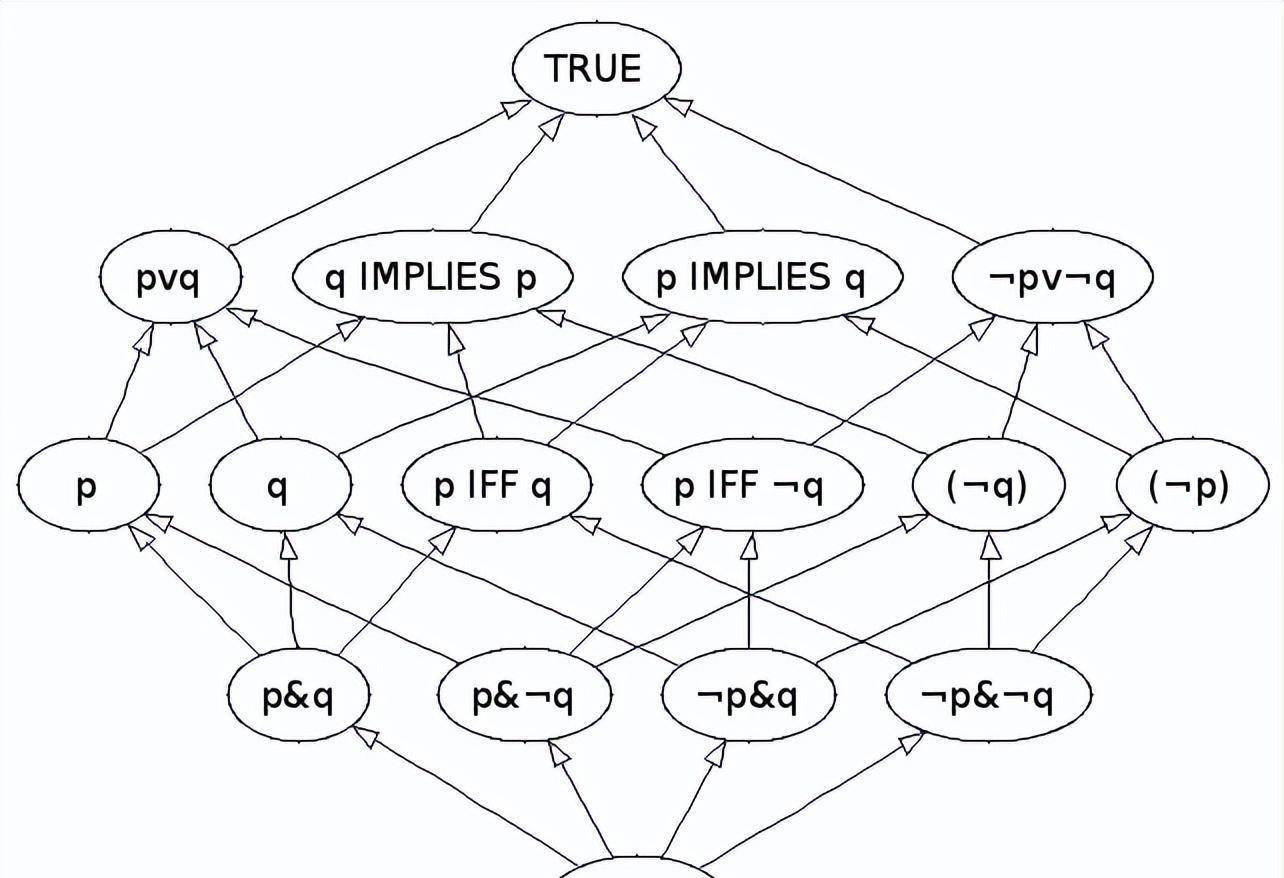
1854年,布尔发表了他最著名的论文,创造了今天计算机和所有电子设备使用的二进制系统。这是对亚里士多德逻辑体系的拓展。“布尔代数”基于亚里士多德的逻辑体系,主要基于两个量:1和0。
在《思想法则》中,布尔还创建了一种概率的通用方法,它可以从任何事件系统的给定概率中,确定与这些事件逻辑相关的任何其他事件的后续概率。
1857年,他被选为皇家学会的会员。两年后,他写了《思想法则》系列的续集《有限差分演算论》,讨论了微分方程的解。

1858年,他获得剑桥哲学学会的荣誉会员资格。第二年,他还被授予牛津大学荣誉学位。1864年12月,布尔冒着一场暴风雨,从家里步行三英里去皇后学院,可能这个原因,他得了肺炎,再也没能康复。那年,他在爱尔兰科克的巴林坦普尔去世,享年49岁。月球上有一个陨石坑以他的名字命名。
他的学术生涯可以用19世纪英国著名数学家、伦敦大学学院数学系教授奥古斯都·德·摩根的话来总结:
布尔的逻辑系统只是天才和耐心结合在一起的众多证明之一……作为数值计算工具而发明的代数符号过程,应该能够表达每一个思想行为,并为一个包罗万象的逻辑系统提供语法和字典,除非得到证明,否则人们不会相信这一点。