字节跳动面试必会：快速选择算法，TopK问题最优解

在面试字节跳动的过程中，现场写算法代码是绕不开的一个环节。其中快速排序(Quick Sort)、快速选择(Quick Select)是最常见的算法题之一。快速选择是目前解决TopK问题的最优算法，如果想拿下字节跳动的offer，快速排序算法是必须要掌握的算法之一！

开篇先出到面试题，请读者思考一下可能的解法：

给你一个无序数组，请找出其中第K大的数，时间复杂度控制在O(N)。

如果不对时间复杂度加约束的情况下，该题有很多种可能解法，例如：

• 用任意一种性能不错的排序算法先将数组进行排序，然后从中找到位置k的数值。但即便用当前最好的排序算法，时间复杂度也是在O(n·log n)的级别，不符合题目要求。
• 用大顶堆算法，仅保留K个最大的值。这种算法的时间复杂度虽然优于前面一种，但时间复杂度也是O(n·log k)的级别，依然不满足题目要求。

因此，为了达到题目中要求，就必须要引出今天的主角：快速选择算法(Quick Select)。快速选择算法是目前解决TopK问题的最优解。其核心思想和快速排序类似，因为这两个经典算法的提出者都是同一个人——C.A.R.Hoare。

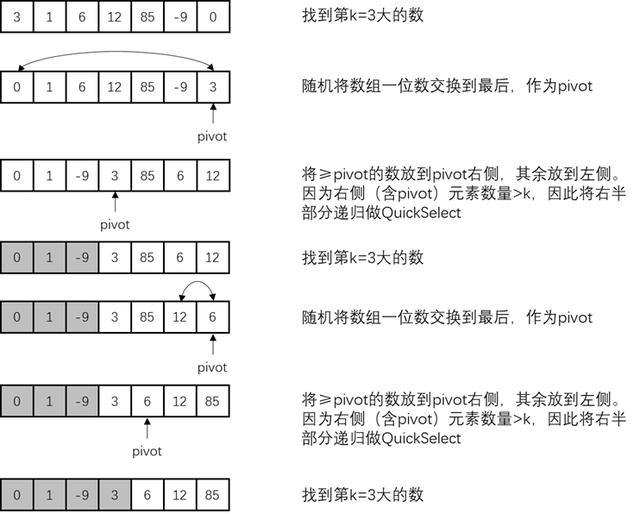
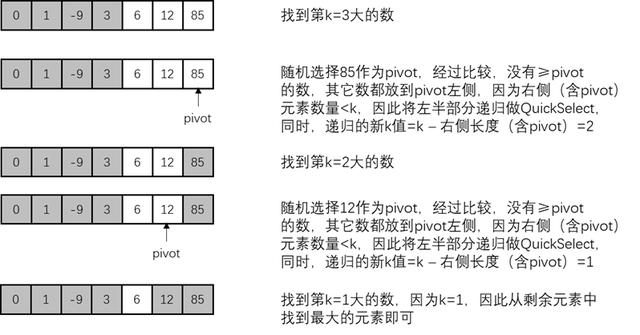
快速选择的执行步骤是先从数组中随机选择一个元素作为pivot，然后遍历数组，将<pivot的元素都放在pivot左侧，≥pivot的元素都放在pivot右侧。如此遍历完以后，如果要找第k大的数，可以判断pivot两侧元素个数。假设pivot右侧元素个数≥k可推断出，第k大的数一定在pivot右侧的元素中，因此拿pivot右侧部分作为新数组重新进行一轮找出第k大元素的快速选择即可。若pivot右侧元素个数<k，可知，第k大的数一定在pivot左侧，因此以pivot左侧所有元素作为新数组，重新进行一轮快速选择，但是k的值就变为k-右侧元素个数，因为最大的若干个元素都在pivot右侧中，所以要从k中减去这些右侧元素的个数。

以下是一个快速选择的示例：

以下是基于JAVA实现的快速选择的代码，仅供参考：

public int findTopK(int[] nums, int k, int start, int end) {
        if (k <= 0) {
            throw new IllegalArgumentException("K can not less than 1!");
        } else if (k > (end - start + 1)) {
            throw new IllegalArgumentException("K out of range! start = " + start + ", end = " + end + ", k = " + k);
        }

        if (k == 1) {
            int max = Integer.MIN_VALUE;
            for (int i = start; i <= end; i++) {
                max = Math.max(max, nums[i]);
            }
            return max;
        }

        int rand = new Random().nextInt(k);
        int tmp = nums[end];
        nums[end] = nums[start + rand];
        nums[start + rand] = tmp;
        int pivot = nums[end];

        int l = start, r = start;
        while (r < end) {
            if (nums[r] > pivot) {
                r++;
            } else {
                tmp = nums[r];
                nums[r] = nums[l];
                nums[l] = tmp;
                l++;
                r++;
            }
        }

        tmp = pivot;
        nums[end] = nums[l];
        nums[l] = tmp;

        if (start + (end - start + 1) - l >= k) {// 若右侧（含l）数量≥k
            return findTopK(nums, k, l, end);
        } else {// 右侧（含l）数量不足k
            return findTopK(nums, k - (end - l + 1), start, l - 1);
        }
    }

快速选择的时间复杂度是O(n)，推论依据是快速选择每次遍历的元素个数预期都会减半，因此全部要遍历的元素个数是：

Sn = n + n/2 + n/4 + …… + 1

这是一个典型的等比数列求和，套用等比数列求和公式可得：

Sn = n + n/2 + n/4 + …… + 1 = (a1 - an · q) / (1 - q)= (n - 0.5) / 0.5 = 2n - 1

去除不必要的常数，仅保留数量级之后可得，快速排序的预期时间复杂度是O(n)

现如今互联网求职竞争越发激烈，难度越发困难，如果不做好充足的复习，很可能会丧失宝贵的面试机会！关注我，定期高频更新优质面试宝典，帮助你在职场中平步青云，斩获理想offer！