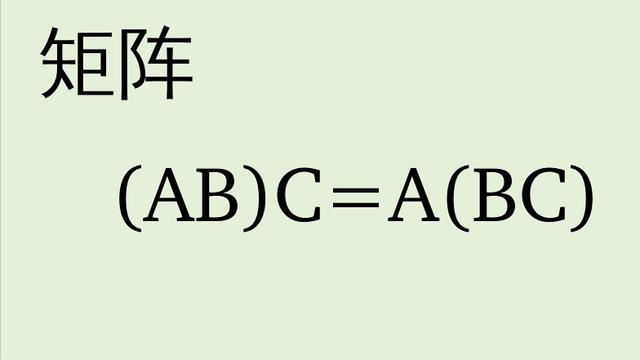矩阵结合律对于如何影响我们的生活，下面是我个人的一点浅薄理解。

• 1、使得计算机设计得更简单。
• 2、加速计算机运算

忙碌的996

初识矩阵时你是否困扰过：为什么搞出矩阵这样的怪物？不易懂，计算繁琐，不够直观？

浮于书本表面很难直接理解它产生的历史原因，直到我做足够多的计算机工程项目后偶然顿悟了。妙呀~数学科学家才是真正的怪物。

写一元一次方程求解，哗啦啦的程序代码巧了一堆。 在遇到二元一次方程求解，又是哗啦啦的一堆。 写梯度下降法，N维空间，若干个for循环语句，写的我晕乎乎的。

最重要的是，上面三个案例代码根本没法复用代码，程序员的996生活由此而来。

更简单

Matlab为什么是工程科学家的伙伴，它利用矩阵的表达方法，将“运算”做了统一，工程科学家只要提供合适的“矩阵描述”，就能得出想要的结果， 将“计算机算法实现”和“工程计算”完全分离。以至于Matlab上运算就如同纸上写表达式一样简单。

更迅速

矩阵运算使得计算方法变得简单后，使得它成为计算机运算基础的可能，虽然这种方法建立在繁琐的逐行乘以逐列的基础上，可以用硬件去实现繁琐的乘法，矩阵乘法AB可以做为计算机最小的运算单元，就好像用二极管的高低电平表达0、1一样。

有了计算机矩阵运算的硬件，接下来的一步是如何能再提高矩阵的运算速度。

看看矩阵有什么奇妙的特性：

• 交换律(AB)C=(AC)B，恩~不支持。
• 结合律(AB)C=A(BC)，不错，幸好支持结合律运算。

下面这张图是直观感受结合律，2x2的三个矩阵验算表达式。

至于推广到任意矩阵去证明，《线性代数与应用》书中证明矩阵结合律过程如下。

好了，既然满足结合律，那么计算机是不是可以用多线程的方式去完成， 比如ABCD这4个矩阵，我是不是可以分割成2个线程去完成?

ABCD=(AB)(CD)

下面随机生成4组44x44的矩阵，Y1、Y2得到结果相同（44x44=1936个位置都相同）。

计算机最适合计算重复的工作，显卡是把重复运算发挥得淋漓尽致的。显卡有若干个流处理器，流处理器可以看成是多个运算器，相当于CPU里的ALU，由于CPU做的是通用运算，要面临多种应用领域，所以ALU设计的比流处理器复杂。个人电脑16核心就嗨上天了，服务器也就100多个核心，而显卡最低端的都有数百个流处理器，NVIDIA AMD高端显卡3000~4000。

线程是应用程序的概念，永远不可能某线程独占CPU处理资源，CPU有调度的过程。而放在显卡流处理器上就不一样的，天生就为矩阵运算而生，(AB)和(CD)划分到两个流处理器上是完全占用流处理器资源的。

矩阵运算可裁剪

还是上面的ABCD运算，如果把矩阵A看成游戏里人物的模型，B看成贴图、C看成贴图模糊、D看成模型高光处理。

那对于运算量不足的计算机就可以选择性地打开和关闭效果。模型高光如火焰效果、某玄幻小说宝物修炼到高等级的特效。

运算量不足的机器可以省略D过程，仅计算ABC，特效除了视觉效果外，不影响游戏的运算逻辑。