还记得计算机网络中的信道复用技术么? 来来来, 一起复习一下.

why

问: 什么是信道复用. 在回答这个问题之前先看这样一个场景:

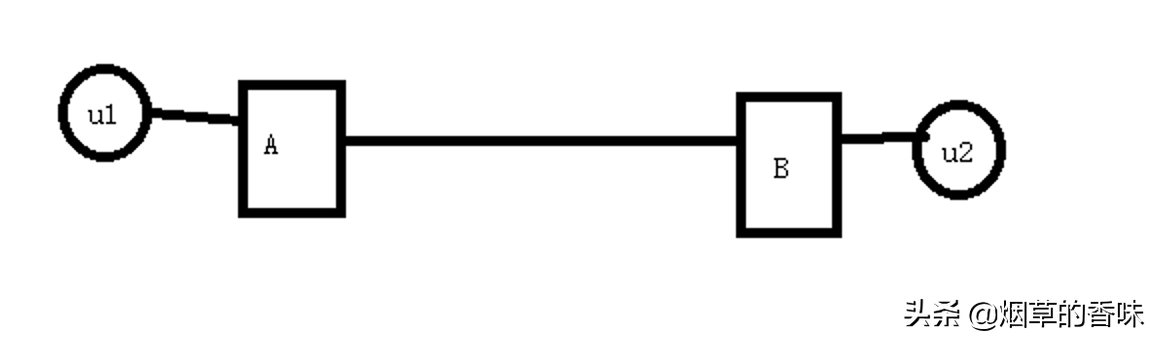
其中u1 u2是两个用户, 如果这两个用户之间连通的信道在他们使用过程中, 被他们完全占用了, 其他人就只能等着了. 那有人说了, 那就多架设信道不就好了. 如果说 A B之间的信道可以满足20G 流量的传输, 而u1 u2 在通信的过程中, 只使用了其中的千分之一, 这就造成了资源的极度浪费, 不管从哪方面考虑, 都应该充分利用其传输的性能.

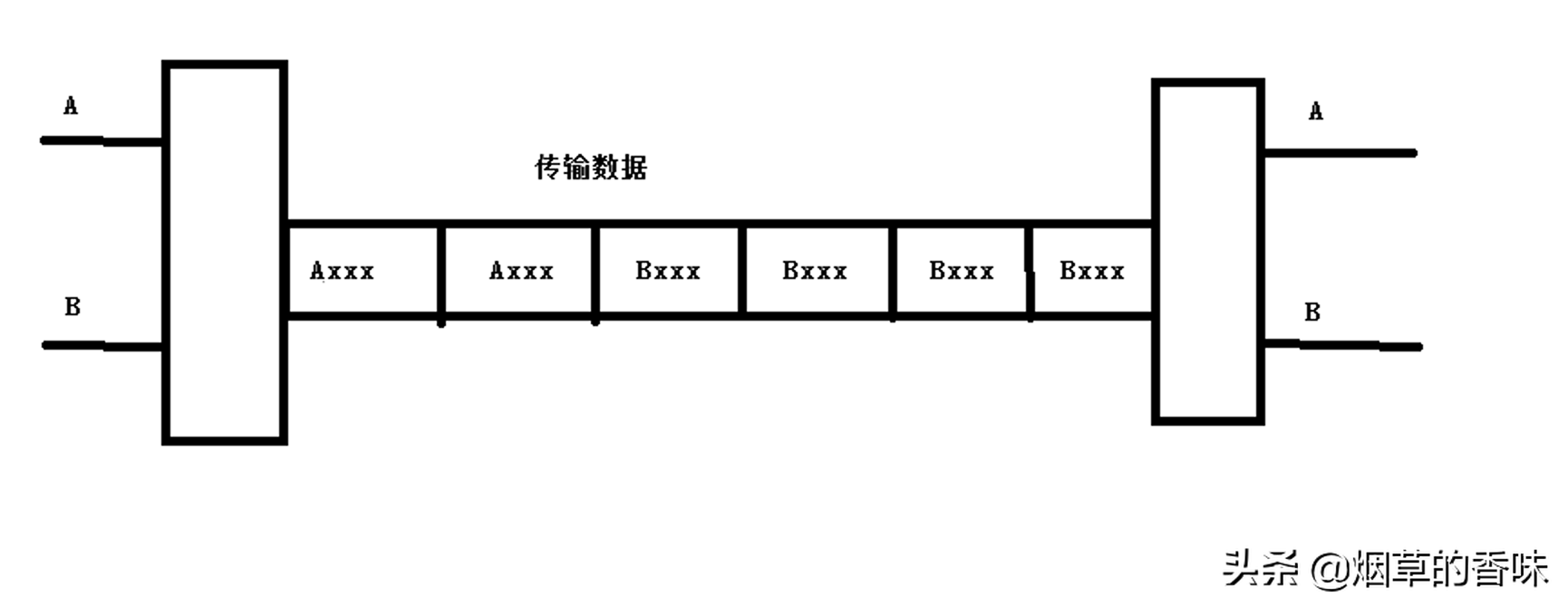
而这个时候, 为了解决这个问题, 就出现了信道的复用技术. 简单说, 就是可以在同一个信道上同时传送多路数据. 如图:

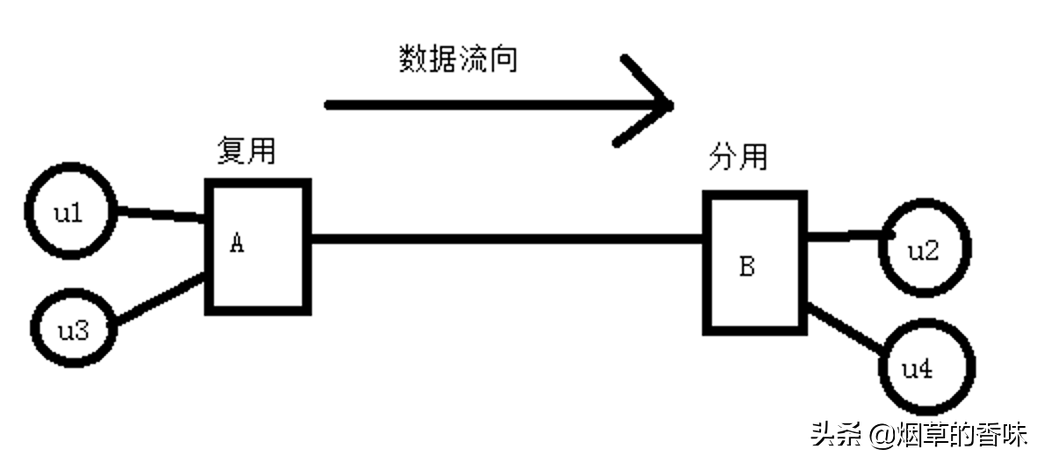
为了方便理解, 将信道转化为单工通信. 其中u1给u2发送数据的同时, u3也可以给u4发送数据. 同一个信道可传输多路信号的通信.

信道复用的基本思路简单说就是, 在发送端将多路信号揉成一个信号发送, 而接收端需要将信号再拆分成各路信号进行分发.

如何实现信道的复用呢?

频分复用

现在最常使用的传输媒介就是光纤了, 都知道光信号有不同的频率, 可见光只占用其中的一小部分.

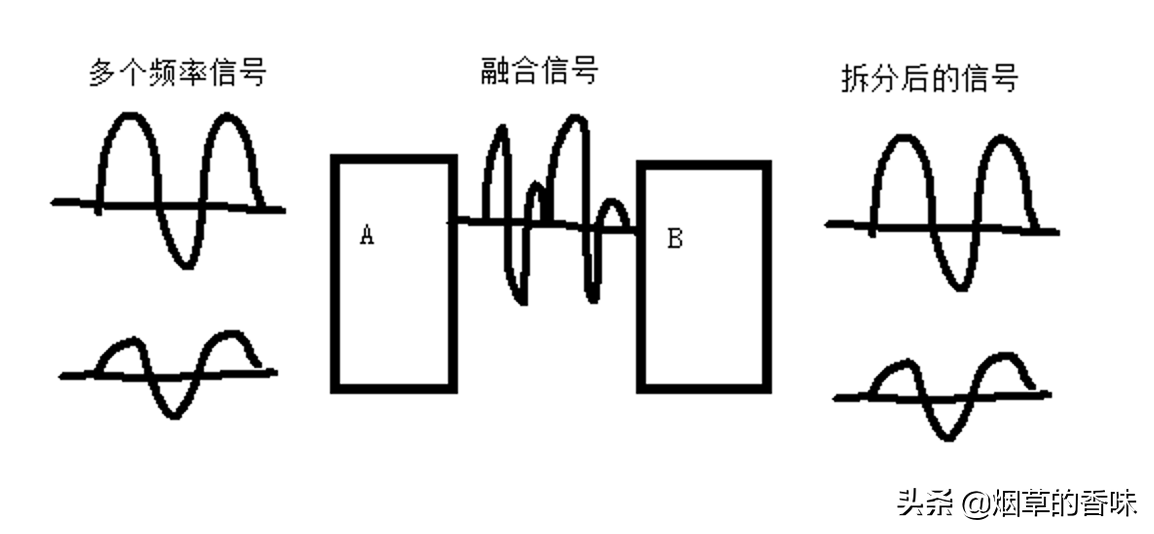
而频分复用, 就是通过将不同频率的信号进行融合, 然后在接收端再进行不同频率信号的分离. 当然, 叠加后的频率是不能超出传输媒介的频率带宽的.

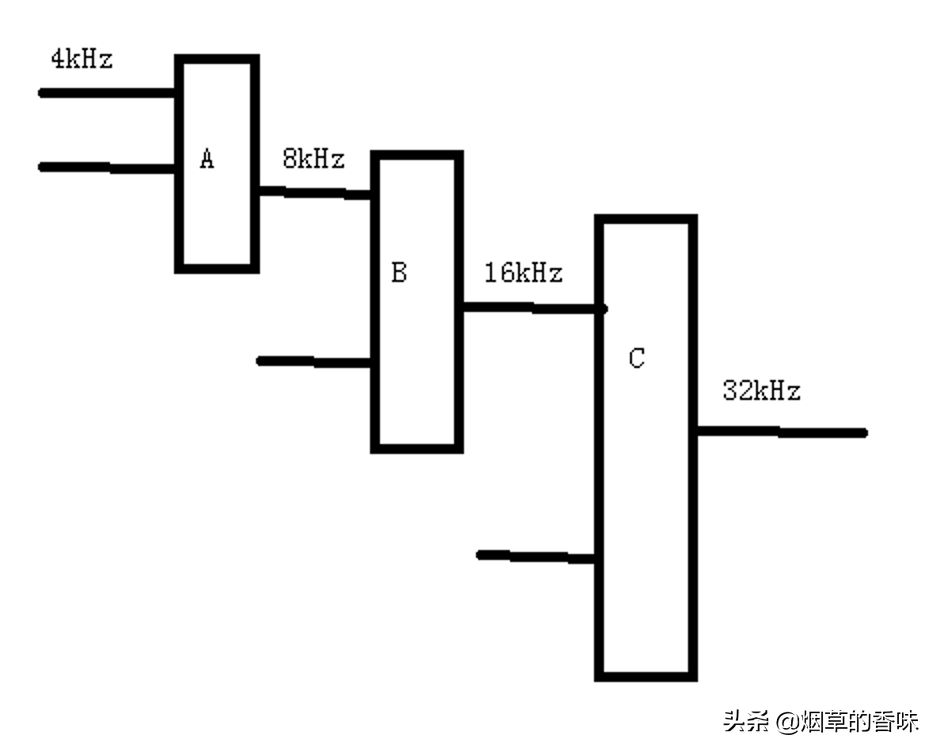
复用技术是可以连续复用的, 从A通过复用, 生成的信号可以在B处再次进行信号的叠加, 而遇到频率带宽低的信道可拆分传输, 最大限度的使用其传输性能.

时分复用

时分复用很好理解, 将信道按照时间段进行划分, 多个输入端轮流发送数据, 接收端再按照时间段将数据进行拆分.

问题

时分复用技术的问题显而易见, 每个输入方占用信道的机会都是均等的. 如果说A没有数据, 为了接收端能够按照时间间隔正确分发数据, A所占用的时间间隔会留空, 造成资源的浪费.

统计时分复用

为了解决时分复用空闲造成的资源浪费, 出现了统计时分复用. 基本思路一致, 也是将信道按照时间间隔进行分割, 不同的是, 每次放入数据的时候, 会携带一个tag, 标记本段数据的所属, 接收端根据tag对分段数据进行识别分发(当然, 接收端同时会将附带的tag去掉). 这样一来, 只要有数据就方, 而不用空出空闲间隔了.

波分复用

波分复用技术说白了, 其实就是频分复用. 都知道, 光是有不同的波长的, 波分复用是根据不同的波长进行复用.

问题是, 光的波长和频率成反比, 波长一定, 频率就也定了. 这这这, 不就是频分复用换了个名嘛. (可能只是因为在复用时用到的技术不同吧)

码分复用

先说一下, 码分复用中的码是什么. 在传输过程中, 将一个比特的时间间隔, 再次切分为 n 个间隔, 其中每个间隔称为一个码片.

每个发送接收方, 定义一个自己的码片序列, 如下:

一共7个码片(也就是说, 原来发送1比特的数据, 现在需要发送7比特). 当发送数据的时候, 如果是二进制1, 就直接发送码片序列, 如果是二进制0, 则将码片序列取反再发送.

那么这个发送的序列如何叠加呢? 很简单, 就是两者波形的叠加. 1+1=2, (-1)+(-1)=-2, -1+1=0. (向量的点积) 叠加后的波形是两个波形的和.

到这里都很好理解, 问题是接收方如何从数据中将波形分离出来呢? 前面的分离都是物理模型, 咱也不太懂, 到这里是数学模型了, 可以简单唠一唠.

先复习一下向量相关的概念

首先, 上方的码片就是一个包含: 1, -1 的向量.

码片向量的规格化内积: 按位相乘, 取平均值. (内积是向量的概念, 就是点积除以 n)

根据这个定义, 有如下推理:

• 任一码片与自身规格化内积为1 (每位都相同, 相乘后均为1, 取平均值任为1)
• 任一码片与其反码片内积为-1 (每位都相反, 相乘后均为-1, 取平均值-1)

正交码片: 内积为0

信号拆分

首先, 容易分离的不同向量必须是正交向量. 证明过程就不说了, 咱也不懂

如何拆分信号呢? 结果很简单, 将收到的信号与自己的码片序列做内积运算, 若内积为0, 则当前比特没有自己的信号, 否则为1或-1, 既1或0.

其他

信道复用技术除了上面几种, 还有: 空分复用等等.

不同的复用技术, 其对应的应用场景不同. 简单回顾一下.