什么是集肤效应？如何降低集肤效应

趋肤效应的影响

在长直导体的截面上，恒定的电流是均匀分布的。对于交变电流，导体中出现自感电动势抵抗电流的通过。这个电动势的大小正比于导体单位时间所切割的磁通量。以圆形截面的导体为例,愈靠近导体中心处,受到外面磁力线产生的自感电动势愈大；愈靠近表面处则不受其内部磁力线消长的影响，因而自感电动势较小。这就导致趋近导体表面处电流密度较大。由于自感电动势随着频率的提高而增加，趋肤效应亦随着频率提高而更为显著。当频率很高的电流通过导线时，可以认为电流只在导线表面上很薄的一层中流过，这等效于导线的截面减小，电阻增大，大大降低了导体材料的有效利用率。

定义

当交变电流通过导体时，导体内部实际上没有任何电流，电流集中在临近导体外表的一薄层 ，这一现象称为趋肤效应（也称集肤效应）。

趋肤效应具体解析

在计算导线的电阻和电感时，假设电流是均匀分布于他的截面上。严格说来，这一假设仅在导体内的电流变化率（di/dt）为零时才成立。另一种说法是，导线通过直流（dc）时，能保证电流密度是均匀的。但只要电流变化率很小，电流分布仍可认为是均匀的。对于工作于低频的细导线，这一论述仍然是可确信的。但在高频电路中，电流变化率非常大，不均匀分布的状态甚为严重。高频电流在导线中产生的磁场在导线的中心区域产生最大的感应电动势。由于感应的电动势在闭合电路中产生感应电流，在导线中心的感应电流最大。因为感应电流总是在减小原来电流的方向，它迫使电流只限于靠近导线外表面处。这样，趋肤效应使导线型传输线在高频（微波）时效率很低，因为信号沿它传送时，衰减很大。

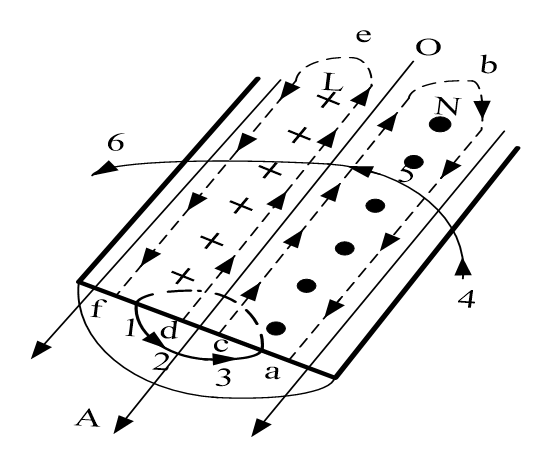
如图所示，当导体通过高频电流i时，变化的电流就要在导体内和导体外产生变化的磁场（图中1-2-3和4-5-6）垂直于电流方向。根据电磁感应定律，高频磁场在导体内沿长度方向的两个平面L和N产生感应电动势。此感应电势在导体内沿长度方向产生的涡流(a-b-c-a和d-e-f-d)阻止磁通的变化。可以看到涡流的a-b和e-f边与主电流O-A方向一致，而b-c边和d-e边与O-A相反。这样的主电流和涡流之和在导体表面加强，越向导线中心越弱，电流趋向于导体表面。这就是趋肤效应。

趋肤深度

由趋肤效应，我们不难联想到另一概念—趋肤深度。工程上定义从导体表面到电流密度下降到导体表面电流密度的0.368（即1/e)的厚度为趋肤深度或穿透深度△，即认为导体表面下深度为△的厚度导体流过导线的全部电流，而在△层以外的导体完全不流过电流（在不规则导体中，考虑趋肤深度以最窄边为准）。△与频率f(w)和导线物理性能的关系为：

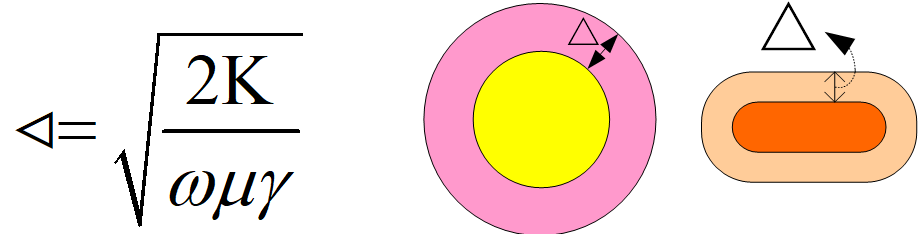
式中，μ-导线材料的磁导率；

γ=1/ρ-材料的电导率；

&KAppa;-材料电导率（或电阻率）温度系数；对于铜μ=

μ0=4π×10-7H/m; 20℃时ρ=0.01724×10-6 Ω/m，电阻率温度系数为1/234.5（1/℃），Κ=（1+（T-20）/234.5）。

T-导线温度（℃）。铜导线温度20℃、不同频率下的穿透深度：

一般磁性元件的线圈温度高于20℃。在导线温度100℃时，ρ100=2.3×10-6 Ω/cm,穿透深度

降低趋肤效应的方法

由于电流趋肤效应的存在，使得导线的有效载流面积减小，导线对交流电流的电阻大于导线的电阻（这里所说的导线的电阻即为导线对直流电流的电阻）；只有导线的趋肤效应面积和导线本身的截面相等时，导线的交流电阻最小，此时有：

Sf =S Rac =Rdc

式中Sf -- 交流趋肤效应面积

S -- 导线截面面积

Rdc -- 导线的直流电阻

Rac -- 导线的交流电阻

因此，减低趋肤效应电阻的最直接的方法，就是改变导线截面的形状，尽量使趋肤效应面积和导线截面面积相同。

(*在计算圆导线和扁导线的交流趋肤效应电阻时，设定趋肤深度条件为小于圆线半径或扁线窄边高度的1/2，在趋肤深度大于这个设定时，计算趋肤效应电阻是无意义的)

1、用多股细线并联代替单根导线来减低趋肤效应的影响：

对于直径为D的圆铜导线，如果传送电流的频率为 f (Hz)，保持交流载流密度Jf 和直流载流密度J 相当，最佳降低趋肤效应电阻的方法是用多股细线替换，使Sf=S，每股细线的直径为：

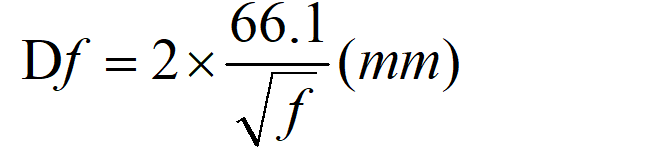
细线的股数为：

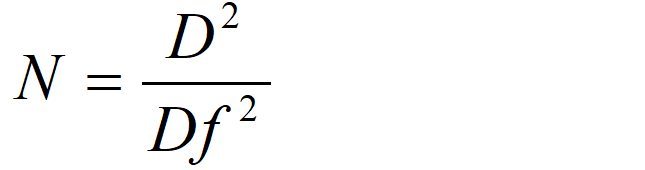
例如，电流 I = 10A，电流密度J = 5.66A/mm2，单股导线的直径为：

导线的直流电阻最为：Rdc =0.01 x L

(*Rdc =ρ x [ 1 + k x ( T -20 ) ] x L / S；

ρ 铜=0.01749Ωm/mm2；k 是导体材料随温度的变化系数，为0.00393) 当电流频率 f = 100kHz时，趋肤效应深度：

趋肤效应面积：Sf =πx ( D - d ) x d=0.8472 mm2

趋肤效应电阻(20℃时)：Rac =0.021 x L （*Rac =ρ x [ 1 + k x ( T -20 ) ] x L / Sf)

交流载流密度：Jf =I/Sf=11.803 A/mm2

用细线代替时，每股线的直径df 和截面积 Sfn为：df =2 x d =0.42 mm

Sfn =πx df 2 / 4 =0.13726 mm2

股数：N =D2 / df 2 =12.87≈13

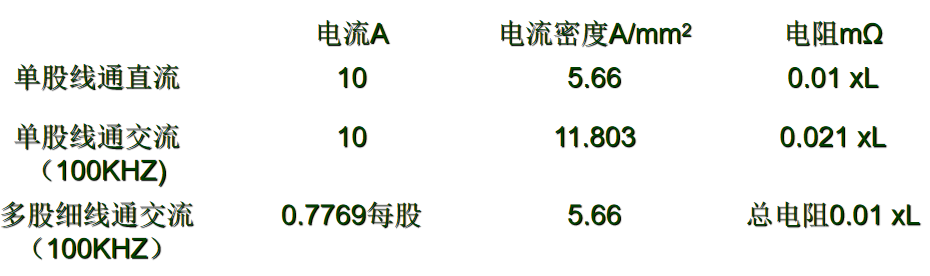
用细线代替后，每股电流 In 和电流密度Jn为：In =I/N=0.7769 A

Jn =In/Sfn=5.66 A/mm2

趋肤效应电阻(20℃时)：Rac =0.01749 x L / ( N x Sfn )=0.01x L≈Rdc

结论：

用1 根1.50mm直径的圆铜线，传送100kHz 10A电流时，电流密度是直流的2.085倍，交流电阻是直流电阻的2.1倍，交流损耗也是直流损耗的2.1倍；使用13根0.42mm直径的圆导线并联来代替1.50mm的单根导线时，交流电阻，电流密度，交流损耗和直径1.50mm的导线的直流电阻，直流电流密度和损耗相当。

2、用带状导线来减低趋肤效应的影响：

在大电流时经常使用扁铜线，在可能的情况下，可以将导线的厚度减小，宽度增加，使其变成带状，只要合理的确定带状线的厚度和宽度，就可以使其高频趋肤效应的影响最小。

根据扁线最佳高度a = 2 x d 的原则，带状铜线的最佳厚度为：

宽度则由要求的电流密度确定。

对于厚度为 a 的带状线，如果传送电流的频率为 f (Hz)，保持交流载流密度Jf 和直流载流密度J 相当，得到最佳减低趋肤效应电阻的带状宽度W是：

例如，电流 I = 100A，电流密度J = 5.0A/mm2，单股扁线的截面积是：

S =I/J=100/5=20.0 mm2

导线的直流电阻最为：Rdc =0.8745 x L mΩ

当电流频率 f = 100kHz时，趋肤效应深度：

如果使用 a=2mm，b= 10mm的扁线时，其有效载流面积为：

Sf =2 x d x ( b + a - 2 x d )=4.842mm2

交流载流密度：Jf=I/Sf =20.65 A/mm2

趋肤效应电阻(20℃时)变为：Rac ≈3.6122 x LmΩ 。

当用带状导线代替扁线时，带的最佳厚度为：a =2 x d =0.42 mm

趋肤效应面积应和扁线面积相同：Sf =a x W =S=20.0mm2

则有带的宽度为：W =S / a≈48 mm

此时，趋肤效应电阻(20℃时)：Rac ≈0.8676 x L mΩ （此时带状导线的截面积为a x W=20.16，所以此时Rac比Rdc稍小一点点）

交流载流密度：Jf=I/S =I/ （a x W）=4.96 A/mm2

带状线(0.42mm x 48mm)的高频电流密度和交流电阻仅为原扁线(2mm x 10mm)的1/4；当然，带状线的交流损耗也仅为扁线的交流损耗的 1/4 。

结论：

扁状导线的趋肤效应电阻和导线的截面形状有关，在截面面积确定后，其窄边高度越大，趋肤效应的影响也越大。

当根据电流的趋肤深度来确定扁线的窄边高度，使扁线变成为厚度等于2倍的趋肤深度，而截面面积和原扁线截面面积相等的带状后，可以使电流趋肤效应的影响减到最小。

3、利用管和泊减低趋肤效应的影响：

在频率很高时（至少大于1KHZ），趋肤效应深度也很小，电流基本集中在导体的表面，内部的导体部分基本上没有电流，将这部分导体去除变成管后，可以大大减轻导体的重量，而对电流的传送又没有影响。同样，在很高的频率时，也可以将带状线压成泊状，既保证其对电流的传送，又可减轻其重量。例如，高频大功率的传输线和高频天线的振子就可以使用铜管或铝管来制作，如果在铜管或铝管的表面加镀一层高导电的金属膜（银或金），效果就会更好；高频传输线或天线，也可以用在不导电的管或棒形胎表面敷（或镀）导电金属泊（膜）来制作，即节省昂贵的金属材料，又保证了导电性能和机械强度。

现在，电子设备的体积越来越小型化，因此电源的工作频率越来越高，为了提高电源中必需的变压器和功率电感的效率，一方面使用高频极低损耗的磁材，一方面使用减低高频电流损耗的导体；比如，目前已广泛生产和使用的极扁带状漆包线就是一种选择。