有时可以将机器学习算法视为一个黑匣子，那么我们如何以更直观的方式来解释它们呢？

在下图中，给定蓝点和红点，我们可以看到有一个图案。 作为人类，我们可以使用"直觉"将它们分开，并预测新点的颜色。

例如，我们大多数人可能会说图中的黑点属于蓝点类别。 但是，如何用数学表达这种"直觉"呢？ 您会发现不同的直觉导致了我们所知道的所有算法……

如果蓝色圆点和红色圆点可能对您来说很抽象，那么让我们来看一些真实的例子。

· 肿瘤的诊断（B代表良性，M代表恶性），具有两种不同的肿瘤特征。

· 垃圾邮件检测：具有两个变量，美元符号的频率和单词"删除"的频率。

您可能已经知道一些可行的分类算法：逻辑回归，kNN，LDA（线性判别分析），SVM，决策树等。

但是了解它们是否直观？

首先，为简化问题，我们将在本文中考虑一维情况（我们将在另一篇文章中考虑二维情况）

如下图所示，我们只有一个预测变量，即X，目标变量是Y，具有两个类别，红点和蓝点。

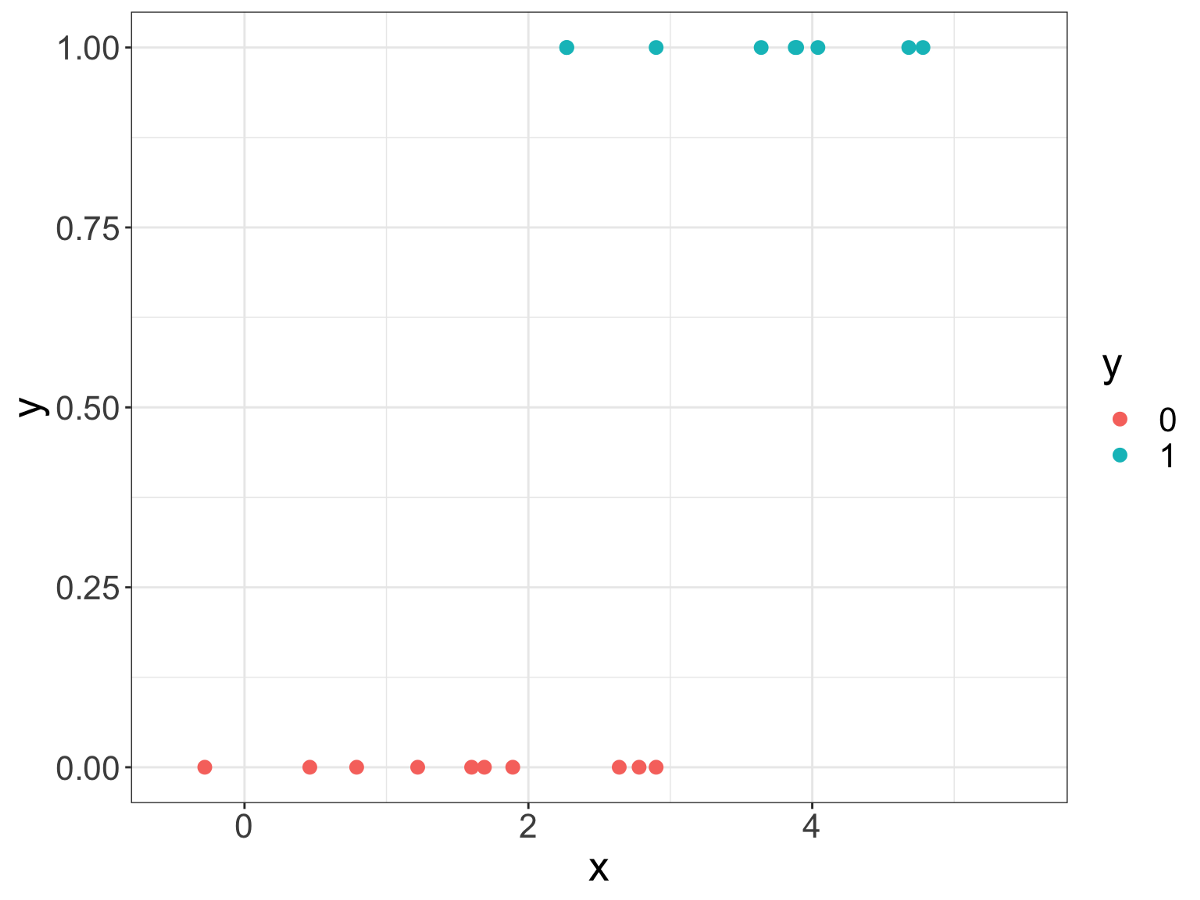
请注意，从数学上讲，"红色"或"蓝色"没有任何意义，因此我们将此变量转换为二进制变量：" 1"代表"蓝色"，" 0"代表"红色"。 这对应于一个问题：点是蓝色的吗？ 1表示True，0表示False。 当然，这只是一个约定。

在真实的单词示例中，"点是蓝色的吗？" 可以是：肿瘤是否恶变？ 电子邮件是否是垃圾邮件？

第一原则：邻居分析

对于给定的点，其想法是查看点的邻居。

邻居是什么？ 最接近的？

"关闭"是什么意思？ 最短的距离？

什么是距离？ 在这里，它仅表示x的两个值之间的差（x是实数）。

现在，给定一个新点，我们可以计算出该点与所有其他点之间的距离。 我们可以选择最接近的。

但是多少？ 这种方法的主要问题是：我们选择多少点？

首先，我们将其称为k，并说k = 5。

现在我们可以检查邻居的阶级。 如果您拥有一类的多数，则可以通过多数类进行预测。 在我们的例子中，如果邻居的多数类为1，则新点很可能属于1类。

注意"多数"原则。 因此，如果我们选择k = 4，那么将很难决定。 因此，如果k为奇数，则有助于做出明确的决定。

现在可以计算出新点的概率了，下面的图形如下：

对于K最近邻，这个原理称为kNN。

现在，此算法的特殊之处在于，由于您不知道要保留哪些点，因此必须为每次预测保留所有这些点。 这就是为什么我们说此算法不是基于模型的，而是基于实例的。

第二条原则：全球比例和正态分布

上面我们刚刚说过，选择数字k很不方便，我们没有对观察结果建模。

那么，现在我们该怎么办？ 首先，让我们考虑所有人口。 如果这样做，则对于所有新点（多数类）的预测都将相同，而概率将是多数类的比例。

这可能有点简单。 为了做得更好，我们可以考虑点的正态分布。 为什么呈正态分布？ 好吧，它很简单，并且简化了所有计算。 这真的是一个很好的理由吗？ 好吧，这就是我们所谓的"建模"。

所有模型都是错误的，但有些是有用的。 —著名的统计学家乔治·博克斯（George Box）

现在，我们不用问邻居，而是可以问一个更好的问题：我离蓝点或红点有多远。 换句话说：给定一个新点，该点是蓝色或红色的概率是多少？

· 新点与蓝点之间的距离有多近？ 我们考虑蓝点的概率密度函数（记为PDF_b），而距离（或更确切地说，接近度）为PDF_b（x）

· 新点与红点之间的距离有多近？ 我们考虑红点的概率密度函数（记为PDF_r），并且距离（或更接近）为PDF_r（x）

为了知道新点更接近哪种颜色，我们只需要比较两个概率密度即可。 在下图中，黑色曲线表示比率：PDF_b /（PDF_b + PDF_r）

现在，在建模方面令人惊奇的是：使用kNN，您必须保留所有点来做出决定，现在只需要使用几个参数（例如均值和标准偏差）来定义 正态分布。

在先前的数据集中，我们有相同数量的蓝点和红点。 如果数量不同，我们可以按比例对两个密度进行加权。

现在，该原理已被以下算法使用：线性判别分析，二次判别分析，朴素贝叶斯分类器。

它们之间有什么区别？

还记得我们必须计算法线密度吗？ 为了获得正态分布，我们必须计算平均值和标准偏差。 对于这种方法，这很容易。 但是对于标准偏差，我们有两种选择。 我们可以计算每个类别的标准偏差，或者为简化起见，我们可以考虑两个类别的标准偏差相同。 为何如此 ？ 我们可以使用两个标准偏差的加权值。 现在为什么要"线性"还是"二次"？ 为此，我们必须查看正态概率密度函数，是的，公式，以及所有指数，平方，pi等。所以让我们再做一次。

那朴素的贝叶斯呢？ 对于一维，LDA和朴素贝叶斯实际上是相同的。 他们又有什么不同呢？ 在下一篇文章中，我们将讨论二维情况。

第三原则：前沿领域分析

根据先前的原理，我们可以看到在对整个数据集建模之后，我们得出了一个决策边界。

现在，我们想知道：如果目标是寻找边界，为什么我们不直接分析边界区域？

可以用M（用于边距）定义"边界区域"，M是我们选择定义"边界区域"的两点之间的距离。 我们可以将红色圆点的候选点标记为A，将蓝色圆点的候选点标记为B。 用数学术语来说，我们有：

M = B-A

首先，让我们考虑一下这两个类是线性可分离的。 然后，我们可以计算出最大的红点（我们得到A）和最小的蓝点（我们有了B）。 （请注意，在一维情况下，最小值和最大值很容易定义。但是，当维数较高时，最大值和最小值可能会更复杂。）

现在非常直观地，我们可以选择两个值的平均值作为决策边界。

但是，如果类0的一个值非常接近类1怎么办？ 然后，我们将具有如下图所示的边界：

现在我们有了这样的直觉，第二种情况下定义的决策边界并不是最佳的：边界区域很小。 现在，如果我们保留先前的M，并让异常指向，该怎么办，如下所示：

并且我们可以为异常点添加一个惩罚项，可以是异常点与A之间的距离。

甚至更好的是，我们可以用系数对惩罚进行加权，并将其称为C。因此，最终决策标准是：

M-C×（红色异常点-S_r）

（保证金减去加权罚款）

通常，如果存在多个异常点，我们可以对所有异常点求和：

M-C×（∑（红色异常点-S_r）+ ∑（S_b-蓝色异常点））

这样，我们还解决了如下图所示的点不可线性分离的情况的问题（请记住，我们说过，我们首先可以考虑点是线性可分离的，以便获得直观的"边界 区域"。）

现在，此原理已用于SVM（支持向量机），为了获得SVM的最终版本，我们必须进行一些小的调整（我们将在另一篇文章中进行讨论）。 为什么将其称为"支持"？ 好吧，因为您使用了不同的点（称为"支持向量"）以最大化边距（或更准确地说是受罚边距）。

原则四：寻找最优曲线

为此，让我们考虑将y建模为x的函数的直线。

y = a×x + b

为了简化此问题的解决，我们可以考虑直线将通过每个类的平均值，如下图所示。

现在，当y = 0.5时可以考虑x的值，这可以作为决定y属于0类还是1类的决策边界。

但是对于这种模型，对于x的大值，您将得到y> 1，对于x的小值，y <0。 所以，我们能做些什么？ 让我们平滑一下。 像这样 ？

来吧，我们可以做得更好，这样吗？

为了进行上图中的平滑处理，我们可以使用例如以下功能

p（x）= 1 /（1 + exp（-（a×x + b）））

要了解为什么使用此函数，您可以注意到我们找到了初始直线：y（x）= a×x + b，我们可以定义：sigma（y）= 1 /（1 + exp（ -y）））

所以我们有：p（x）= sigma（y（x））= 1 /（1 + exp（-（a×x + b）））

为了可视化平滑效果，我们可以在下面看到sigma的图形

· 当x非常大时，输出非常接近1

· 当x很小时，输出非常接近0

现在的任务是查找参数：a和b。 为了实现这一目标，我们可以考虑对每个点进行正确分类的概率。

· 对于蓝点，概率值为p（x）；

· 对于红点，概率值为1-p（x）。

准则是总概率的最大化：我们将所有概率（对于0类和1类）相乘。 并且我们尝试使结果最大化。

P_overall =乘积（类别1为p（x））×乘积（类别0为（1-p（x））

或更简单的形式

P_overall =乘积（p（x）×y +（1-p（x））×（1-y））

然后，数学上的技巧是取对数并取导数等。但是事实证明，没有一种简单的方法（封闭式）可以找到参数，而我们必须用数值方法求解。

下面我们可以看到a和b不同值的情况。 垂直线段代表每个点的概率。 所有这些概率的乘积应最大化，以优化a和b。

这就是逻辑回归使用的原理，因为我们之前看到过sigma函数的名称，称为逻辑函数。

（如果您发现此解释不够直观，则可以阅读本文：直观地讲，我们如何（更好）理解逻辑回归）

第五原则：避免错误

最终原则是关于选择决策边界时可能犯的错误。

现在有什么错误：

· 如果在该区域中有多数蓝点，则红点是错误；

· 如果红色点占多数，则蓝色点就是错误。

找到决策边界后，点将分为两个区域。 想法是描述区域的"均匀性"：错误越少，就越好。

现在，让我们找到一个描述区域"同质性"的函数。 例如，考虑p作为1类的比例。 并且我们得到（1-p）对于类别0的比例。

现在有了p和（1-p），我们能做什么？ 让我们从非常简单的操作开始。

· 总和？ 嗯，再想一想。

· 产品。 嗯，这是一张图表。

因此该函数是对称的，这是必需的特性，因为此函数应适用于任何一个类。 此函数的输出可以指示区域的"均匀性"：越低越好

· 当p接近1时，几乎所有的点都是蓝色的，该指示器非常低

· 当p接近0时，几乎所有点都被撕裂，则指示器也非常低

· 当p为0.5时，我们有相同数量的红点和蓝点，这不是所需的状态。 该指标处于最高水平。

为了找到决策边界，我们必须测试x的不同值。 对于x的每个值，将创建两个区域：左侧区域和右侧区域。 对于每一侧，我们可以计算指标，然后用每个区域中点的比例对它们进行加权，以获得总体指标。

现在我们可以测试所有点作为决策边界，并查看指标如何变化。

现在我们可以采用指标的最低级别来找到x的最佳值。 请注意，由于我们具有阶跃函数，因此我们可以计算x的两个值的均值，以定义指标的最低水平。

现在，此原则的特别之处在于，您可以继续在每个区域中找到其他决策边界。 我们将在另一篇专门讨论该原理的文章中看到，这样做的好处是您可以轻松处理非线性情况。

因此，我们可以一步一步地找到最佳边界。

在这里，我们有关于每个步骤不同决策边界的决策树。

现在的问题是：我们什么时候停止？ 可能有不同的规则……

该原则也被认为是"分而治之"。 它允许增长决策树。 这些树也是更复杂算法（例如，Random Forest或Gradient Boosting machines）的基础。

当我们谈论机器学习和人工智能时，我们总是谈论神经网络，但是为什么我们在这里没有提到它们呢？ 好吧，实际上，我们确实看到了一个简单的神经网络示例，即逻辑回归…

对于机器学习从业者，您可能会注意到，我自愿不使用技术术语，也许您可以在适当的上下文中注释和放置技术术语：硬边距，软边距，梯度下降，凸度，超平面，先验概率，后验概率 ，损失函数，交叉熵，最大似然估计，过度拟合…

让我们回顾一下：

· 原则1：检查邻居，我们得到KNN

· 原则2：考虑全球比例和正态分布，我们可以进行LDA，QDA或NB。

· 原则3：研究边界区域，并尝试使其"干净"且大。 我们得到了SVM。

· 原则4：画一条直线，使其平滑并尝试调整。 我们得到逻辑回归

· 原则5：分而治之。 我们得到决策树。

请注意，我们并未完成五项原则的所有推理：

· 用kNN确定k in

· 决策树中的停止规则

· 系数C的确定

· 确定逻辑回归的a和b

(本文翻译自Angela Shi的文章《Intuitively, How Can We Understand Different Classification Algorithms Principles》，参考：
https://towardsdatascience.com/intuitively-how-can-we-understand-different-classification-algorithms-principles-d45cf8ef54e3)