Transformer它就是个支持向量机

编辑：蛋酱、小舟

SVM is all you need，支持向量机永不过时。

Transformer 是一个支持向量机（SVM）一种新型理论在学界引发了人们的讨论。

上周末，一篇来自宾夕法尼亚大学、加州大学河滨分校的论文试图研究大模型基础 Transformer 结构的原理，其在注意力层的优化几何与将最优输入 token 与非最优 token 分开的硬边界 SVM 问题之间建立了形式等价。

在 hackernews 上作者表示，这种理论解决了 SVM 将每个输入序列中的「好」标记与「坏」token 分开的问题。该 SVM 作为一个性能优异的 token 选择器，与传统为输入分配 0-1 标签的 SVM 本质上不同。

这种理论也解释了注意力如何通过 softmax 引起稀疏性：落在 SVM 决策边界错误一侧的「坏」token 被 softmax 函数抑制，而「好」token 是那些最终具有非零 softmax 概率的 token。还值得一提的是，这个 SVM 源于 softmax 的指数性质。

论文上传到 arXiv 上面之后，人们纷纷发表意见，有人表示：AI 研究的方向真是螺旋上升，难道又要绕回去了？

绕了一圈，支持向量机还是没有过时。

自经典论文《Attention is All You Need》问世以来，Transformer 架构已为自然语言处理（NLP）领域带来了革命性进展。Transformer 中的注意力层接受一系列输入 token X，并通过计算

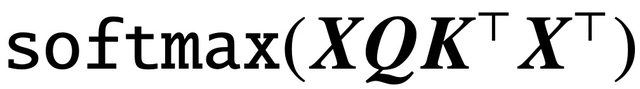
评估 token 之间的相关性，其中 (K, Q) 是可训练的 key-query 参数，最终有效捕获远程依赖关系。

现在，一篇名为《Transformers as Support Vector machines》的新论文在自注意力的优化几何和 hard-margin SVM 问题之间建立了一种形式等价，使用 token 对的外积线性约束将最优输入 token 与非最优 token 分开。

论文链接：https://arxiv.org/pdf/2308.16898.pdf

这种形式等价建立在 Davoud Ataee Tarzanagh 等人的论文《Max-Margin Token Selection in Attention Mechanism》的基础上，它能够描述通过梯度下降进行优化的 1 层 transformer 的隐式偏差（implicit bias）：

(1) 优化由 (K, Q) 参数化的注意力层，通过消失正则化（vanishing regularization），收敛到一种 SVM 解决方案，其中最小化组合参数

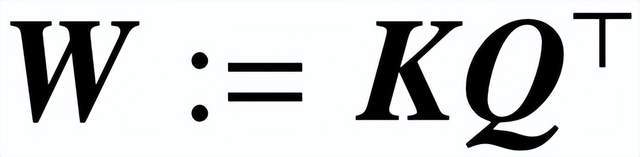
的核范数（nuclear norm）。相反，直接通过 W 进行参数化可以最小化 Frobenius 范数 SVM 目标。该论文描述了这种收敛，并强调它可以发生在局部最优方向而不是全局最优方向。

(2) 该论文还证明了 W 参数化在适当的几何条件下梯度下降的局部 / 全局方向收敛。重要的是，过度参数化通过确保 SVM 问题的可行性和保证没有驻点（stationary points）的良性优化环境来催化全局收敛。

(3) 虽然该研究的理论主要适用于线性预测头，但研究团队提出了一种更通用的 SVM 等价物，可以预测具有非线性头 / MLP 的 1 层 transformer 的隐式偏差。

总的来说，该研究的结果适用于一般数据集，可以扩展到交叉注意力层，并且研究结论的实际有效性已经通过彻底的数值实验得到了验证。该研究建立一种新的研究视角，将多层 transformer 看作分离和选择最佳 token 的 SVM 层次结构。

具体来说，给定长度为 T，嵌入维度为 d 的输入序列

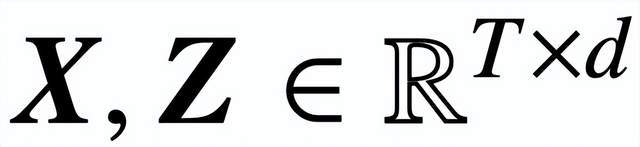
，该研究分析核心交叉注意力和自注意力模型：

其中，K、Q、V 分别是可训练的键、查询、值矩阵，

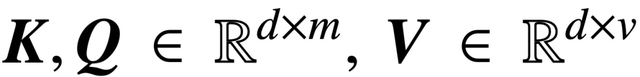
；S (・) 表示 softmax 非线性，它逐行应用于

。该研究假设将 Z 的第一个 token（用 z 表示）用于预测。具体来说，给定一个训练数据集

，

，

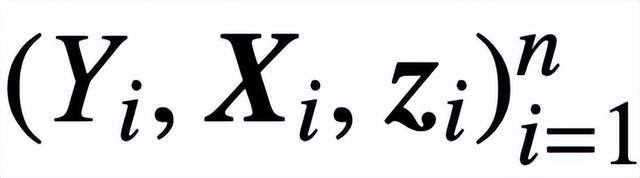
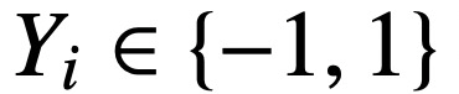
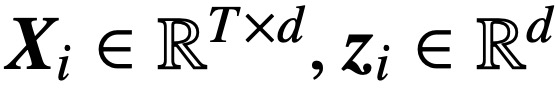
，该研究使用递减损失函数

进行最小化：

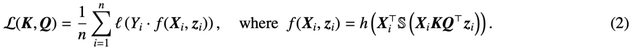
这里，h (・) ：

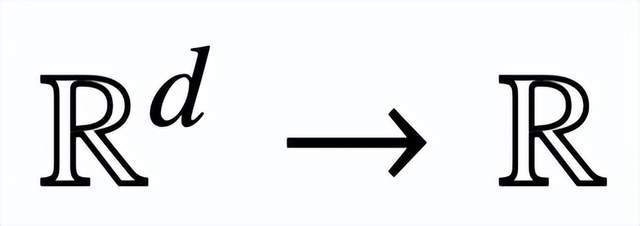
是包含值权重 V 的预测头。在这种表述中，模型 f (・) 精确地表示了一个单层 transformer，其中注意力层之后是一个 MLP。作者通过设置

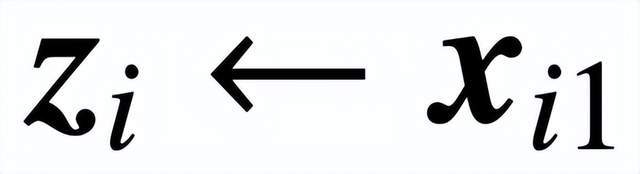
来恢复 (2) 中的自注意力，其中 x_i 表示序列 X_i 的第一个 token。由于 softmax 运算的非线性性质，它给优化带来了巨大挑战。即使预测头是固定和线性的，该问题也是非凸和非线性的。在本研究中，作者将重点放在优化注意力权重（K、Q 或 W）上，并克服这些挑战，从而建立 SVM 的基本等价性。

论文结构如下：第 2 章介绍了自注意力和优化的初步知识；第 3 章分析了自注意力的优化几何，表明注意力参数 RP 收敛到最大边际解；第 4 章和第 5 章分别介绍了全局和局部梯度下降分析，表明 key-query 变量 W 向 (Att-SVM) 的解决方案收敛；第 6 章提供了在非线性预测头和广义 SVM 等价性方面的结果；第 7 章将理论扩展到顺序预测和因果预测；第 8 章讨论了相关文献。最后，第 9 章进行总结，提出开放性问题和未来研究方向。

论文的主要内容如下：

注意力层的内隐偏差（第 2-3 章）

正则化消失的情况下优化注意力参数（K, Q），会在方向上收敛到

的最大边际解，其核范数目标是组合参数

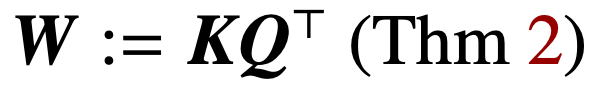
。在直接用组合参数 W 对交叉注意力进行参数化的情况下，正则化路径 (RP) 定向收敛于以 Frobenius 范数为目标的（Att-SVM）解。

这是第一个正式区分 W 与（K，Q）参数化优化动态的结果，揭示了后者的低阶偏差。该研究的理论清楚地描述了所选 token 的最优性，并自然地扩展到了序列到序列或因果分类设置。

梯度下降的收敛（第 4-5 章）

通过适当的初始化和线性头 h (・)，组合 key-query 变量 W 的梯度下降（GD）迭代在方向上收敛到（Att-SVM）的局部最优解（第 5 节）。要实现局部最优，所选 token 必须比相邻 token 得分更高。

局部最优方向不一定是唯一的，可以根据问题的几何特征来确定 [TLZO23]。作为一项重要贡献，作者确定了保证向全局最优方向收敛的几何条件（第 4 章）。这些条件包括：

• 最佳 token 在分数上有明显区别；
• 初始梯度方向与最佳 token 一致。

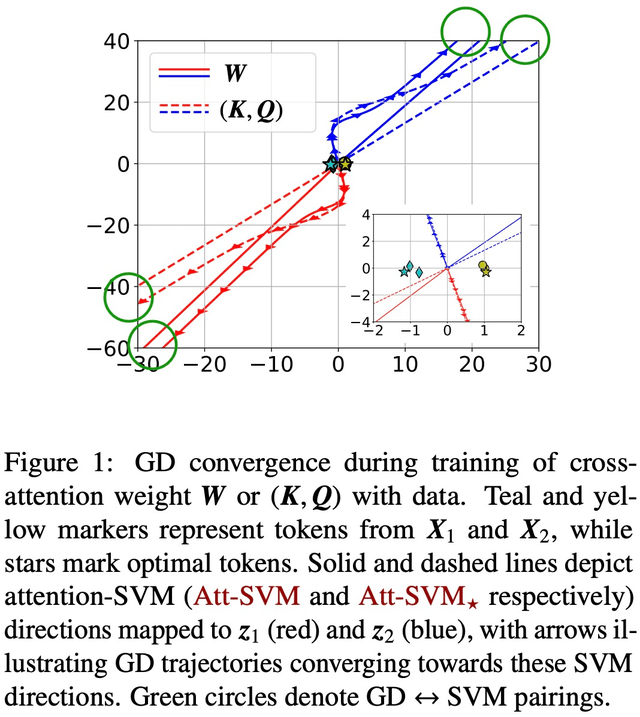
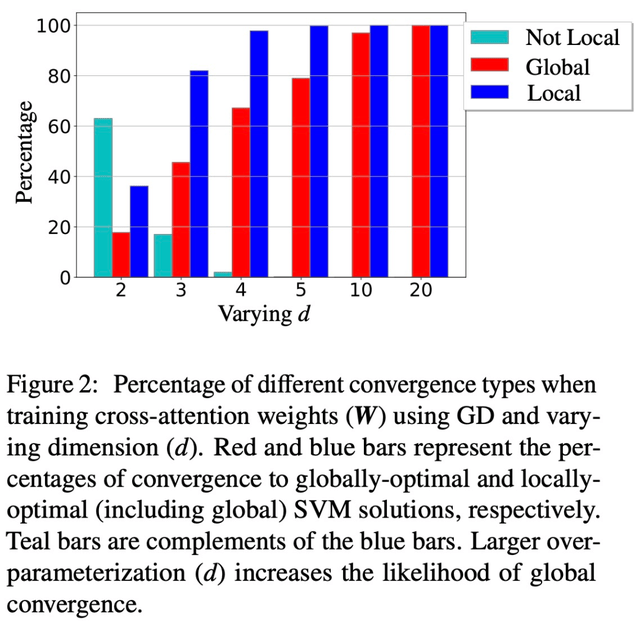
除此以外，论文还展示了过度参数化（即维度 d 较大，以及同等条件）通过确保（1）（Att-SVM）的可行性，以及（2）良性优化 landscape（即不存在静止点和虚假的局部最优方向）来催化全局收敛（见第 5.2 节）。

图 1 和图 2 对此进行了说明。

SVM 等价的通用性（第 6 章）

当使用线性 h (・) 进行优化时，注意力层会固有地偏向于从每个序列中选择一个 token（又称硬注意力）。这反映在了 (Att-SVM) 中，表现为输出 token 是输入 token 的凸组合。与此相反，作者表明非线性头必须由多个 token 组成，从而突出了它们在 transformer 动态过程中的重要性（第 6.1 节）。利用从理论中获得的洞察力，作者提出了一种更通用的 SVM 等价方法。

值得注意的是，他们证明了在理论未涵盖的普遍情况下（例如，h (・) 是一个 MLP），本文的方法能准确预测通过梯度下降训练的注意力的隐含偏差。具体来说，本文的通用公式将注意力权重解耦为两个部分：一个是由 SVM 控制的定向部分，它通过应用 0-1 掩码来选择标记；另一个是有限部分，它通过调整 softmax 概率来决定所选 token 的精确组成。

这些发现的一个重要特点是，它们适用于任意数据集（只要 SVM 可行），并且可以用数字验证。作者通过实验广泛验证了 transformer 的最大边际等价性和隐含偏差。作者认为，这些发现有助于理解作为分层最大边际 token 选择机制的 transformer，可为即将开展的有关其优化和泛化动态的研究奠定基础。

参考内容：

https://news.ycombinator.com/item?id=37367951

https://Twitter.com/vboykis/status/1698055632543207862