概念

维基百科中对于回溯算法的定义：

回溯法 采用试错的思想，它尝试分步地去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效地正确地解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况：

• 找到一个可能存在的正确的答案；
• 在尝试了所有可能的分步方法后宣告该问题没有答案

关键词：深度优先、递归、尝试各种可能、回退、遍历（暴力解法）

回溯与动态规划的区别

共同点：

用于求解多阶段的决策问题。多阶段决策问题即：

• 求解一个问题分为很多步骤（阶段）；
• 每一个步骤（阶段）可以有多种选择。

不同点：

• 动态规划只需要求我们评估最优解是多少，最优解对应的具体解是什么并不要求。因此很适合应用于评估一个方案的效果；
• 回溯算法可以搜索得到所有的方案（当然包括最优解），但是本质上它是一种遍历算法，时间复杂度很高。

相关经典算法题

鲁迅说过，算法学习，七分练，三分学。接下来就让我们一起来康康常见的几个题目吧～

全排列

leetcode 46:

输入: [1,2,3]
输出: [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]]

回溯算法思路：

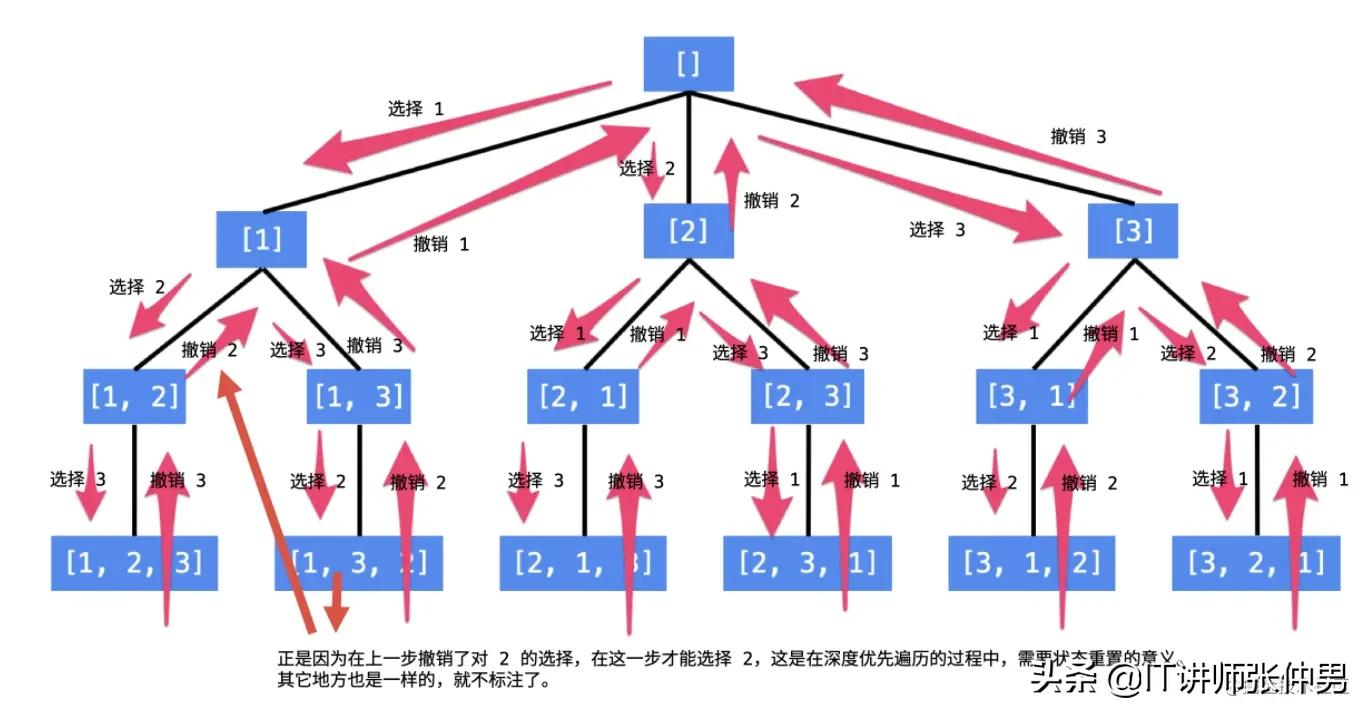
说明：

• 每一个结点表示了求解全排列问题的不同的阶段，这些阶段通过变量的「不同的值」体现，这些变量的不同的值，称之为「状态」；
• 使用深度优先遍历有「回头」的过程，在「回头」以后， 状态变量需要设置成为和先前一样 ，因此在回到上一层节点的过程中，需要撤销上一次的选择，这个操作称之为「状态重置」；
• 深度优先遍历，借助系统栈空间，保存所需要的状态变量，在编码中只需要注意遍历到相应的结点的时候，状态变量的值是正确的，具体的做法是：往下走一层的时候，path 变量在尾部追加，而往回走的时候，需要撤销上一次的选择，也是在尾部操作，因此 path 变量是一个栈；
• 深度优先遍历通过「回溯」操作，实现了全局使用一份状态变量的效果。

使用编程的方法得到全排列，就是在这样的一个树形结构中完成 遍历，从树的根结点到叶子结点形成的路径就是其中一个全排列。所以，树的最后一层就是递归终止条件。

代码实现：

var permute = function(nums) {
  let len = nums.length, res= [];
  if(!len) return res;

  let used = []; // boolean[]
  let path = []; //number[]
  dfs(nums, len, 0, path, used, res);
  return res;

  function dfs(nums, len, depth, path, used, res){
      if(depth === len) {
          //path是动态数组，不能直接push，需要拷贝一份当前值保存到结果中
          res.push([...path]); 
          return;
      }
      
      // 针对全排列中下标为depth的位置进行所有可能的尝试
      for(let i=0; i<len; i++){
          if(!used[i]){
              path.push(nums[i]);
              used[i] = true;

              // 往下找全排列中的下一个位置
              dfs(nums, len, depth+1, path, used, res);

              // 形成一个全排列后，进行回退，尝试其他答案
              used[i] = false;
              path.pop();
          }
      }
  }
};
复制代码

• 首先这棵树除了根结点和叶子结点以外，每一个结点做的事情其实是一样的，即：在已经选择了一些树的前提下，在剩下的还没有选择的数中，依次选择一个数，这显然是一个 递归 结构；
• 递归的终止条件是： 一个排列中的数字已经选够了 ，因此我们需要一个变量来表示当前程序递归到第几层，我们把这个变量叫做 depth，或者命名为 index ，表示当前要确定的是某个全排列中下标为 index 的那个数是多少；
• 布尔数组 used，初始化的时候都为 false 表示这些数还没有被选择，当我们选定一个数组的时候，就将这个数组的相应位置设置为 true ，这样在考虑下一个位置的时候，就能够以 O(1) 的时间复杂度判断这个数是否被选择过，这是一种「以空间换时间」的思想。

这些变量称为「状态变量」，它们表示了在求解一个问题的时候所处的阶段。需要根据问题的场景设计合适的状态变量。

N皇后

leetcode 51 如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击

输入：4
输出：[ [".Q..", Q","Q...","..Q."], ["..Q.","Q...", "...Q", ".Q.."] ]

• 遍历每一行的每一列，如果当前位置不会产生攻击就记录当前位置并结束本行循环，往下一行走；如果本行没有一个位置能安放，或者已经走完所有行，就回退到上一个安放的位置，继续看此处的下一个位置能否安放，往复循环。
• 那么，重点是怎么判断当前位置能否安放，在循环中，一行只能放一个，放下之后就立马进入下一行，所以一行中不会有重复的项，那列和对角线呢？我们使用三个数组来分别记录列和主副对角线的使用情况，当某个位置放下一个皇后之后，记录该列到列数组中，此后该列不能使用；
• 关于对角线：

主对角线规律：x-y=k（行-列=固定值）
副对角线规律：x+y=k（行+列=固定值）
所以，当某个位置放下一个皇后之后，记录当前行+列的值，和行-列的值，此后的位置如果行+列或行-列有与数组中重复的，都不可使用。

代码实现：

var solveNQueens = function(n) {
  if(n==0) return res;

  let col = [], mAIn = [], sub = []; // boolean[]
  let res = []; // string[]
  let path = []; //number[]
  dfs(0, path);
  return res;

  function dfs(row, path){
      // 深度优先遍历到下标为 n，表示 [0.. n - 1] 已经填完，得到了一个结果
      if(row == n){
          const board = convert2board(path);
          res.push(board);
          return;
      }

      // 针对下标为 row 的每一列，尝试是否可以放置
      for(let j=0; j<n; j++){
          if(!col[j] && !main[row-j+n-1] && !sub[row+j]){
              path.push(j);

              // 记录该位置的攻击范围
              col[j] = true;
              main[row-j+n-1] = true; //加n-1是为了防止数组索引为负数
              sub[row+j] = true;

              // 进入下一行
              dfs(row+1, path);

              // 回溯, 去掉path中最后一个值，尝试其他选项
              col[j] = false;
              main[row-j+n-1] = false; 
              sub[row+j] = false;
              path.pop();
          }
      }
  }

  // 输出一个结果
  function convert2board(path){
      let board = []; // string[]
      for(let i=0; i<path.length; i++){
          let ret = new Array(n).fill('.');
          ret[path[i]] = 'Q';
          board.push(ret.join(''))
      }
      return board;
  }
};
复制代码

回溯算法解题模板

通过以上几个问题不难发现，回溯算法解题的要点就是要定义好状态变量，不断对状态进行推进、回退，尝试所有可能的解，并在状态处于递归树的叶子节点时输出此时的方案。

// 简单模版
function backtrack(){
  let res = [];
  let used = [];

  function dfs(depth, path){ // depth表示当前所在的阶段
    // 递归终止条件
    if(depth === len){
      res.push(path);
      return;
    }

    // 针对当前depth尝试所有可能的结果
    for(let i=0; i<len; i++){
      if(!used[i]){ // 此路不通的标记
        path.push(nums[i]);
        used[i] = true;

        // depth+1 前往下一个阶段
        dfs(depth+1, path);

        // 重置本阶段状态，尝试本阶段的其他可能
        used[i] = false;
        path.pop();
      }
    }
  }
}