JAVA基于分治算法实现的棋盘覆盖问题示例

本文主要介绍了ava基于分治算法实现的棋盘覆盖问题,简单描述了棋盘覆盖问题,并结合具体实例形式分析了java基于分治算法实现棋盘覆盖问题的相关操作技巧,需要的朋友可以参考下

分治算法是用了分治思想的一种算法，在进行了解棋盘问题前，我们先了解一下什么是分治？

将父问题分解为子问题同等方式求解，这和递归的概念很吻合，所以在分治算法通常以递归的方式实现(当然也有非递归的实现方式)。分治算法的描述从字面上也很容易理解，分、治其实还有个合并的过程：

• 分(Divide)：递归解决较小的问题(到终止层或者可以解决的时候停下)
• 治(Conquer)：递归求解，如果问题够小直接求解。
• 合并(Combine)：将子问题的解构建父类问题

一般分治算法在正文中分解为两个即以上的递归调用，并且子类问题一般是不想交的(互不影响)。当求解一个问题规模很大很难直接求解，但是规模较小的时候问题很容易求解并且这个问题并且问题满足分治算法的适用条件，那么就可以使用分治算法。

在一个2^k * 2^k个方格组成的棋盘中，有一个方格与其它的不同，若使用以下四种L型骨牌覆盖除这个特殊方格的其它方格，如何覆盖。四个L型骨牌如下图：

棋盘中的特殊方格如图：

实现的基本原理是将2^k * 2^k的棋盘分成四块2^(k - 1) * 2^(k - 1)的子棋盘，特殊方格一定在其中的一个子棋盘中，如果特殊方格在某一个子棋盘中，继续递归处理这个子棋盘，直到这个子棋盘中只有一个方格为止如果特殊方格不在某一个子棋盘中，将这个子棋盘中的相应的位置设为骨牌号，将这个无特殊方格的了棋盘转换为有特殊方格的子棋盘，然后再递归处理这个子棋盘。以上原理如图所示：

具体代码如下：

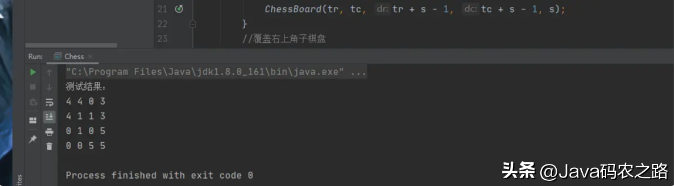
package demo;public class Chess {  /*tr表示棋盘左上角行号  tc表示棋盘左上角列号  dr表示特殊棋盘的行号  dc表示特殊棋盘的列号*/  public static void ChessBoard(int tr, int tc, int dr, int dc, int size) {    if(size == 1) {      return;    }    int t = title ++;    int s = size/2;    //覆盖左上角子棋盘    if(dr < tr + s && dc < tc +s) {      //特殊方格在此棋盘中      ChessBoard(tr, tc, dr, dc, s);    }    else {      //此棋盘中无特殊方格，用t号L型骨牌覆盖右下角      Board[tr + s - 1][tr + s -1] = t;      //覆盖其余方格      ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);    }    //覆盖右上角子棋盘    if(dr < tr + s && dc >= tc + s) {      //特殊方格在此棋盘中      ChessBoard(tr, tc+s, dr, dc, s);    }    else {//此棋盘中午特殊方格，用t号L型骨牌覆盖左下角      Board[tr + s - 1][tc + s] = t;      //覆盖其余方格      ChessBoard(tr, tc + s, tr + s - 1, tc + s, s);    }    //覆盖左下角子棋盘    if(dr >= tr + s && dc < tc +s) {      //特殊方格在此棋盘中      ChessBoard(tr + s, tc, dr, dc, s);    }    else {      //此棋盘中无特殊方格，用t号L型骨牌覆盖右上角      Board[tr + s][tr + s -1] = t;      //覆盖其余方格      ChessBoard(tr, tc, tr + s , tc + s - 1, s);    }    //覆盖右下角子棋盘    if(dr >= tr + s && dc >= tc + s) {      //特殊方格在此棋盘中      ChessBoard(tr + s, tc+s, dr, dc, s);    }    else {//此棋盘中无特殊方格，用t号L型骨牌覆盖左上角      Board[tr + s ][tc + s] = t;      //覆盖其余方格      ChessBoard(tr + s, tc + s, tr + s , tc + s, s);    }  }   @SuppressWarnings("static-access") public static void mAIn(String args[]) {     System.out.println("测试结果：");     Board[2][2] = 0;     Chess ch = new Chess();     ch.ChessBoard(0, 0, 2, 2, size);     for(int i = 0; i < size; ++ i) {       for(int j = 0; j < size; j++) {         System.out.print(Board[i][j] + " ");       }       System.out.println();     }   }  static final int size = 4;  static int title = 1;  static int Board[][] = new int[size][size];}复制代码

运行结果：