程序算法——递归

一、什么是递归?

当函数的定义中，其内部操作又直接或间接地出现对自身的调用，则称这样的程序嵌套定义为递归定义。

递归通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，从而大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。用递归思想写出的程序往往十分简洁易懂。

二、递归的应用

用递归算法求x！

当x=0时，x！= 1

当x>0时， x！=x*(x-1)!

根据数学中的定义把求x！定义为求x*(x-1)!，其中求（x-1)!仍然用求x！的方法，需要定义一个求x！的函数，逐级调用此函数。

假设x=3时，3！=3*2*1=6，它执行的流程图如图：

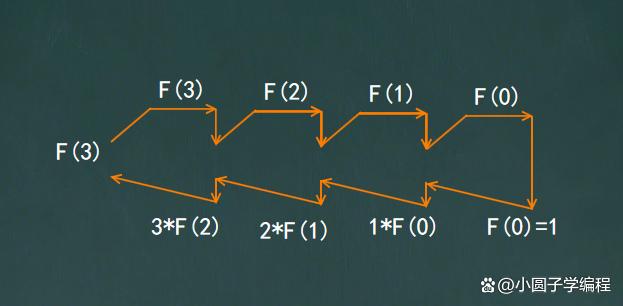
编写的程序如下：

#include <IOStream>

using namespace std;

int t;

int f(int);

int mAIn()

{

int x;

cin >> x;

f(x);

cout << t <<endl;

return 0;

}

int f(int x)

{

if( x == 1)

t = 1;

else

{

f( x-1 );

t = t * x;

}

}

从上面这个例子中可以知道，递归算法的本质就是自己调用自己，用调用自己的方法去处理问题，可使解决问题变得简洁明了。

1、递归程序在执行过程中，一般具有如下模式：

①　将调用程序的返回地址、相应地调用前的变量都保存在系统堆栈中，

②　执行被调用的函数；

③　若满足退出递归的条件，则退出，并从栈顶上弹回返回地址，取回保存起来的变量值，继续沿着返回地址向下执行程序；

④　否则继续递归调用，只是递归调用的参数发生变化：增加一个量或减少一个量，重复执行直到递归调用结束。

2、能够用递归算法解决的问题，一般满足如下要求：

①　需要求解的问题可以化为子问题求解，其子问题的求解方法与原问题相同，只是规模上的增加或减少

②　递归调用的次数是有限的，必须有递归结束的条件。

一个经典的益智游戏——汉诺塔，就是典型的递归算法：

有A、B、C三个塔座和n个大小不一样的圆盘子，需要把A、B、C三个塔座上的盘子利用中间B座，把所有盘子从A盘移动到C盘，规则是每次只允许移动一个盘子，并且在移动过程中，3个座上的盘子始终保持大盘在下，小盘在下。

分析如下：

当盘子数n=1时，只需移动一次：A--->C。

当盘子数n=2时，需要移动三次：A--->B，A--->C，B--->C。

当盘子数n=3时，需要移动7次：A--->C，A--->B，C--->B，A--->C，B--->A，B--->C，A--->C。

由以上分析可知：如果盘子数为n时，则移动的次数为2n-1.

那么如何编写一个盘子数为n的程序呢？我们利用递归的算法来设计程序，你会发现，要把A座上的n个盘子以B座为中转移动到C座，可以分为以下3个步骤来完成：

1、将A座上的n-1个盘子，以C座为中转，移到B座上。

2、把A座上最低下的一个盘子移到C座上。

3、将B座上n-1个盘子，以A座为中转，移到C座上。

可以发现步骤1和3是和原问题本质相同的子问题（规模数量少了1），不停地递归下去，直到当子问题的规模数为1时，只需执行第1个步骤。

这是盘子n=3时，递归算法运行的过程：

图中的数字顺序表示程序运行的顺序。

程序代码可以看我主页里分享的视频。