

MD5(Message-Digest Algorithm 5) ,是一种使用广泛的信息摘要算法,是在1992年由美国的密码学家罗纳德·李维斯特首次提出。
为什么有人认为是可以用来加密,有人却认为是散列呢?到底为什么呢?
那么MD5算法到底是什么?我们可以将MD5算法看做是一台处理机器,可以将计算机中种任意的数据放入这台机器中,然后经过这台机器处理之后,就会产生一个固定长度为128比特的MD5加密的值,传入这个机器的可以是字符串,也可以是一张图片,还可以是一段视频。
可以看出来上面的这个操作是一个典型的哈希函数式的操作方式,可以将任意的数据内容变成一个固定长度的散列值,同一个输入,得到的输出结果始终是相同的,而不同的输入,得到的输出结果也是一样的。

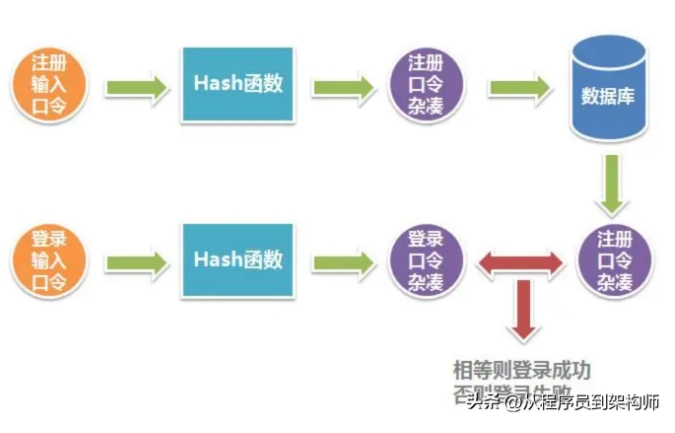
根据这样的特性,我们可以用它来验证一个文件是否被修改过了,或者是可以用它来完成用户登录操作用户名和密码的计算等等。
但是就是这样一个被广泛使用的加密算法,却被人证明已经不再安全了。这到底是怎么回事呢?
为什么MD5算法已经被证明不再安全了,但是还是有很多人在使用呢?这就要从MD5算法的原理讲起了。
MD5算法生成一个MD5的值,可以分为三个步骤。
填充对齐
我们知道在计算机中存储的数据最终都是以二进制的0和1的方式进行存储的。那么当我们拿到一个数据之后第一步需要做的事情就是对数据进行补齐。
举个例子,假设我们得到了715个Bit的数据那么这个时候,就需要将其补齐为512的整数倍数,这里我们发现715Bit离1024Bit比较近,那么,就需要补上309个Bit,让其达到1024Bit。然后在用于补齐的数据中最后的64Bit用来表示原始数据的大小。中间剩余的位置从原始数据开始计算,第一个位置填1,其余的位置全部是0。
当然有一种情况,假设,原始数据大小就是接近了1024这个时候并不能填充64个Bit来表示原始数据大小那么该怎么办呢?那么这个时候,就需要将其补齐到下一个512的倍数,这个也就是1536Bit,然后再按照上面的方法进行补齐。
那么也就是说无论最终数据的大小是多少,只要无法保证上述条件的满足,就需要进行补齐,即使得到的数据恰好是512的整数倍数,我们依然也要进行上述的操作。补齐之后,就需要进行第二步操作分块。
分块
因为通过数据补齐操作,已经将数据补齐成了512的整数倍,所以就一定可以将这些数据以512的大小分为若干的数据块,而我们知道MD5值最后的输出是一个128Bit的固定大小。作者将这128个Bit分成了四个部分。并且通过幻数为这四个部分设置了初始值。
为什么是幻数呢?原因很简单就是为了让你猜不到。
这样分块也就完成了。接下来就是多轮压缩了。
多轮压缩
经过上面的操作,我们可以将数据最终分成两个大块,并且我们将其中一个大块数据拿出来,与上面128Bit的四个分块的值,这里我们标记位A、B、C、D四个值,然后分别用这四个值与数据块分别进行一系列的或与非以及移位运算。这个过程总共进行四轮。然后每轮压缩操作之后,就需要分别更新A、B、C、D的值,那么经过四轮计算之后四个值一共被更新了十六次。
完成压缩操作之后,就将A、B、C、D四个值按照顺序放回到原来的位置上,这个时候散列值就被更新完成了。
这个过程之所以被称为是压缩,实际上就是将512Bit的数据变成了128Bit四个位置中的某个位置,从512到128,信息被压缩了。所以整个的过程被称为是压缩。
然后继续用第二个大块重复上述的工作,这个时候唯一不同的就是128Bit的四个数据值变成了第一个大块数据计算之后的结果。
如果后续的大块数据还有很多,那么操作还是跟上面的操作是一样的。
当我们完成了所有数据的压缩操作,那么散列值就被更新成了最终的结果。整个MD5加密算法的实现过程是有点复琐碎的,但是理解起来并不是太复杂。即使使用比较复杂的面向对象的编程语言也可以在百行代码之内实现它。
既然我们知道了MD5算法的实现细节,那么接下来我们就来看看MD5是如何被攻破的?
在进行攻击之前,首先要搞清楚的就是攻击目标是什么?不然攻击也就没有意义了。根据上面的分析我们知道MD5就是一个产生MD5值的计算函数,而并非对数据进行了加密。所以对于MD5的攻击,其实并非是通过一个密钥去进行解密。
这个很容易理解,密文之所以能成为密文,前提肯定是信息没有损失,如果有损失的话就无法通过密文获取到明文了。显然MD5并不是这样。
宏观上来看,MD5加密之后一个500M的数据被最终压缩成了128个Bit,然后你想用128Bit的数据恢复500M的数据,傻子才会相信呢?从微观的角度上来看,很明显我们在进行补齐操作和分块操作以及后来的数据压缩操作的过程中明显已经改变的数据信息本身,显然是无法直接进行恢复的。这也就导致MD5值的生成过程是一个不可逆的过程。
那么我们还攻击个啥呢?
上面我们知道了,MD5值是通过一个消息数据计算得到的,并且在数学中我们也知道,如果是一个标准的一次函数f(x)=x这种形式的话,那么一个x就对应一个y的值。也就是说一个消息也就对应了一个唯一的MD5的值。
假设 hello 对应的MD5值是123aba123dddaa3,那么也就是说在hello不变的情况下,MD5的值也是不会发生变化的。但是真的是这样么?
上面我们提到任意的输入都会得到一个唯一的输出,其实这句话包含了两个限定条件。
那么在数学概念上来讲,假设有100个房子,也就是说MD5值已经被穷举了,那么有500个人,很显然,肯定会有多个人住一个房子呀,也就是说很明显,一个MD5的值可以对应多个输入的结果呀!
这样一来,上面我们假设的f(x)=x 的函数操作就是有问题的。那么既然产生了哈希冲突了,在MD5中称为是碰撞,那么既然无穷对有界,那么对应的无穷也应该是无穷个。只不过,由于数据处理的缘故,我们无法找到产生碰撞的数据罢了。起码作者在设计MD5的时候可能还没有想到这一点。
所以显然就不存在通过MD5值进行逆向的操作了。
既然一个MD5对应了无穷的消息,那么我们是否可以找到一个或者是我们可以穷举的几个能够产生这样的MD5值的消息呢?很显然,这只是在理论上可行。但实际操作上,这是不行的,穷举就是一个不可能完成的操作,毕竟数量级再那里放着2的128次方,相当于大海捞针。
是不是就没有办法了呢?
假设我们给定了一个消息“Hello World!”,那么它对应的MD5值我们是可以知道的。那么我们可不可以再找到另外的一个MD5值与之相同的数据呢?在MD4中,面对一些弱口令的时候,这种方式是可行的,但是在MD5中,这种方式还是有点难度的。
其实让MD5破防的真正原因其实是下面的这个操作。
我们不需要给定MD5值,也不需要去找到对应的消息,我们只需要制定一个规则,而这个规则就是能够由两个消息,产生同一个MD5就可以了。那么这个时候,操作就简单多了。例如一个二次函数就会出现两个X值对应一个Y值的情况呀!我们不需要找到无数个,只需要找到两个即可。当然这只是一个简单的例子。
那么如何是实现这个操作呢?
很抽象,与产生MD5值的过程相比,这个过程看似简单,实则非常复杂。实际上这也会是信息安全领域的一个关键,打破这个规则往往要比制定这个规则要复杂的多得多。
当然上面的操作只是在实验室给出的操作。但是在真实的工程使用场景中来看,这种方式到底有什么用途呢?
虽然可以找到最终的碰撞值,但是这个碰撞值是通过差分路径和消息的修改而得到的,所以说,最终得到的值也只是一个值罢了,在工程上并没有实际的用处,但事实并非如此。
到此为止,我们知道MD5已经不再安全了,
假设,通过选择前缀方式,生成了两个MD5值相同,但是执行效果完全不同的软件,这个时候,通过MD5校验之后并不会发现两个文件会有什么异常,但是你在选择的时候,正好就选择了哪个带有木马病毒的文件,这个时候,就会出现安全问题了。
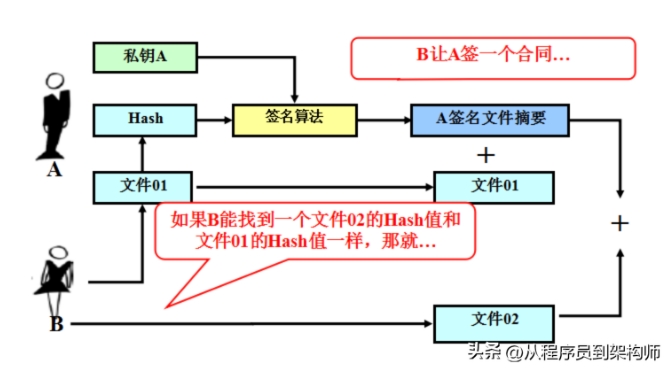
在如果,张三和李四,以MD5作为某个关键文件的真伪验证方式,那么很明显通过选择前缀的方式张三可以提前就制作出来两个MD5值相同的文件,这样在两个文件内容完全是不一样的,但是MD5值却是一样的,最终产生的结果就是被骗了?
那么什么是选择前缀呢?
理解起来其实非常简单,在上面的内容中,我们知道了,如果一个文件大小如果正好是512的话,那么很显然,需要进行补齐操作,这个时候按照规则,补齐之后,文件后面跟的内容正好就是一串没有意义的文件。那么如何让这个文件产生一个MD5值一样的其他文件呢?
通过上面的方式,我们可以知道,在大批量的数据中去找碰撞的话有点难度,不妨我们让文件内容是一样,只让其中的一部分数据发生变化。这样可以很容易就找到碰撞了,这就有点类似于,我们将一个函数的定义域给缩小了,这样在这个小范围定义域中去找到一个碰撞值,就会很简单了。
文章篇幅很长,相信看到这里,可能有点迷糊了!不过能认真看完一定会对你理解MD5 算法有所帮助。