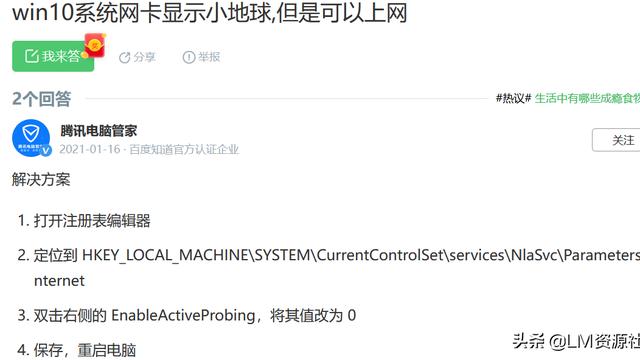
有高中学生经常问我们物理老师:为什么行星绕太阳运动的轨道是椭圆？是圆不更香吗？嘿嘿，这个问题不说高中学生，我们作为老师都整不明白。作为一种学习，我在这篇文章里来详解这个为什么。
开普勒三大定律是德国天文学家开普勒提出的关于行星运动的三大定律。第一和第二定律发表于1609年，是开普勒从天文学家第谷观测火星位置所得资料中总结出来的；第三定律发表于1619年。这三大定律又分别称为椭圆定律、面积定律和调和定律。
开普勒定律
①椭圆定律：所有行星绕太阳的轨道都是椭圆，太阳在椭圆的一个焦点上。
②面积定律：行星和太阳的连线在相等的时间间隔内扫过的面积相等。
③调和定律：所有行星绕太阳一周的时间(即周期)的平方与它们轨道半长轴的立方成正比。
此后，学者们把第一定律修改成为：所有行星（和彗星）的轨道都属于圆锥曲线，而太阳则在它们的一个焦点上。第二定律只在行星质量比太阳质量小得多的情况下才是精确的。如果考虑到行星也吸引太阳，这便是一个二体问题。第三定律也有修正。
太阳系示意图(俯视)
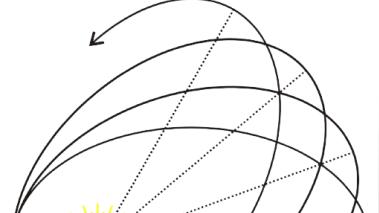
首先我们复习一下矢量的微分和求导。如下图。
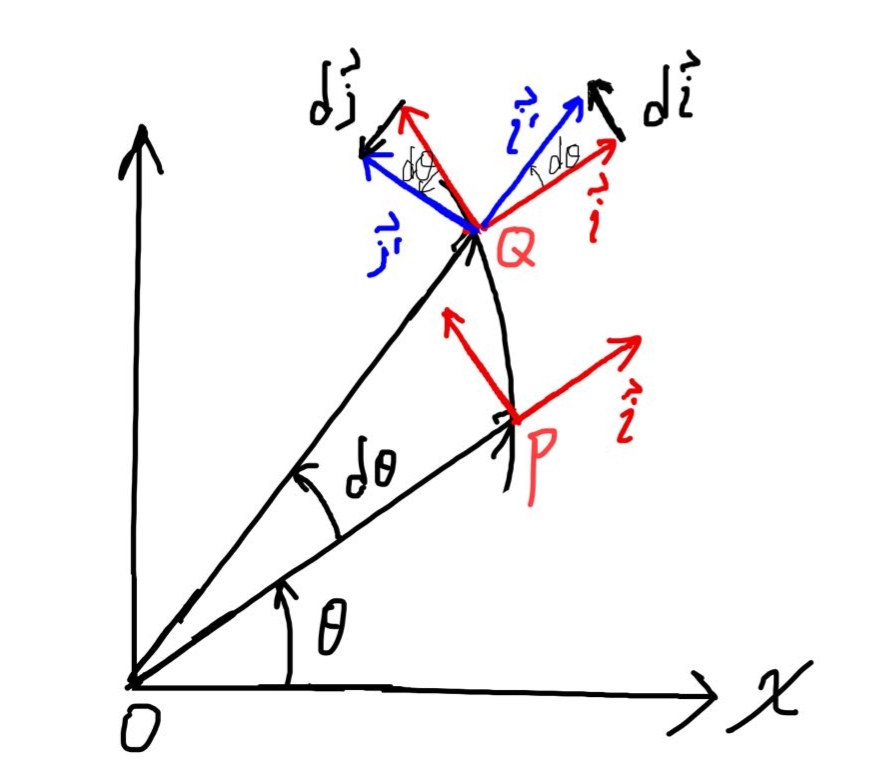
质点在极短时间dt内从P点运动到Q点，其极角也从θ转到θ+dθ，径向单位矢量ⅰ和横向单位矢量J也都转过θ
从这张图里我们可以推导出质点的加速度分解成的横向加速度(垂直于极径)和径向加速度。为此我们先看看上图中橫向单位矢量和径向单位矢量对时间求导会得出什么。
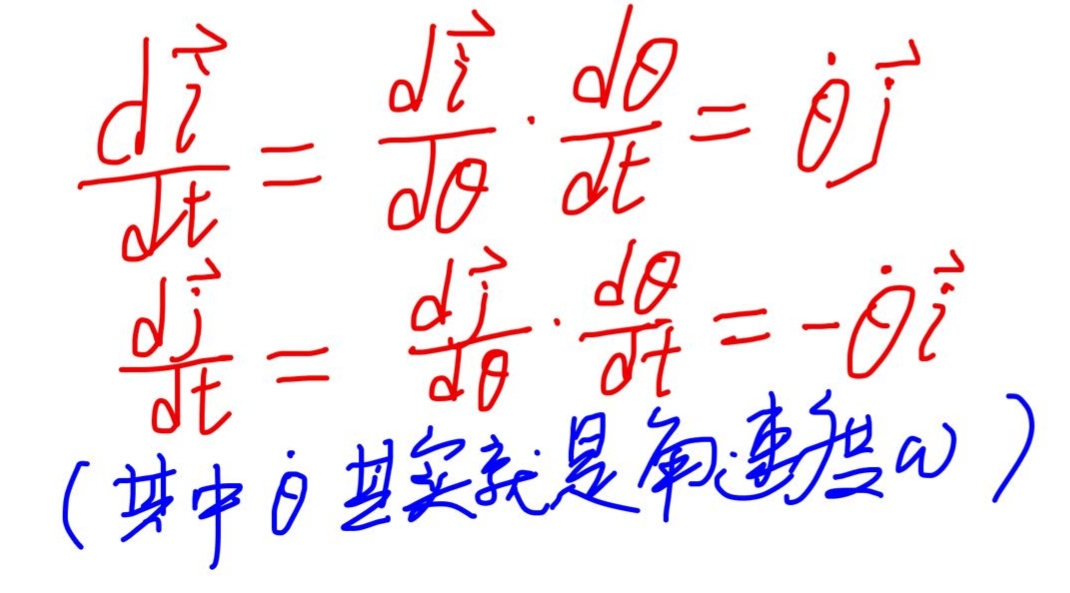
可见，这其实就是两个单位矢量的旋转
然后我们使用高中学的加速度定义:加速度就是速度的变化率，即速度矢量的导数，位移(矢径)矢量的二阶导数。
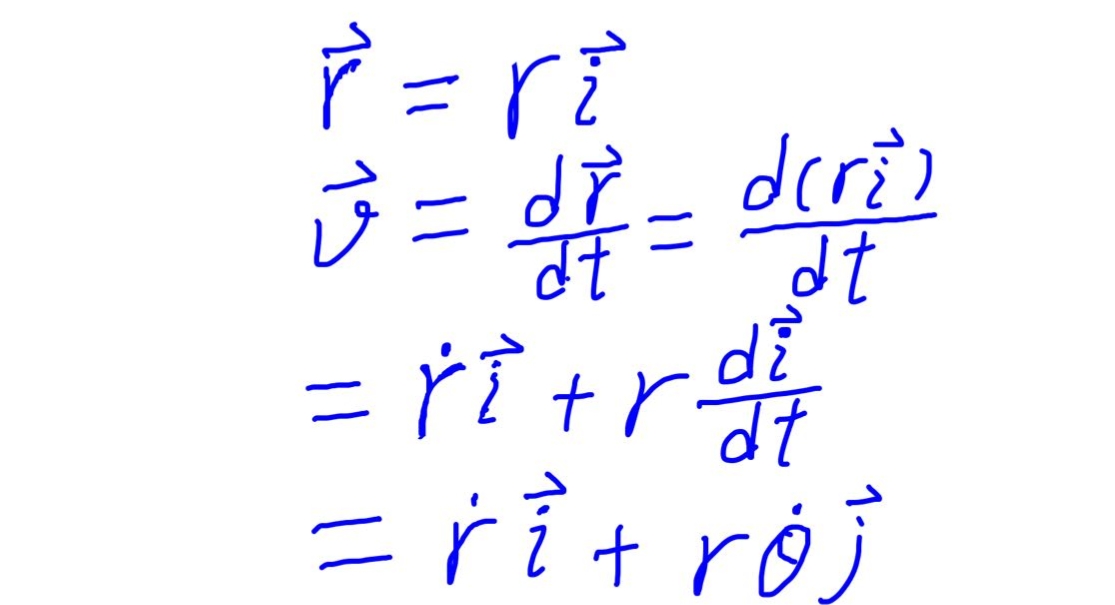
我们都知道，地球所受到的太阳引力是径向的，是始终指向太阳中心的，这就决定了两件事:第一，上式中的径向加速度只需乘上地球质量m就等于地球受到的引力，当然考虑二矢量的方向刚好相反要加上负号才相等。第二，横向加速度(注意不是切向加速度，而是与矢径垂直的方向上的加速度)始终等于零。
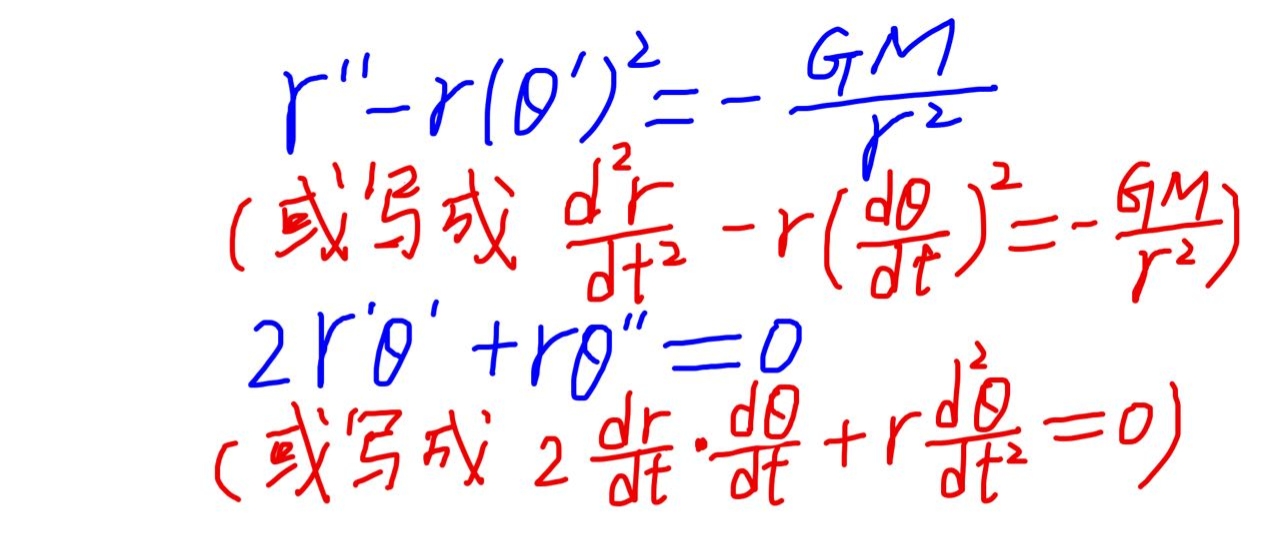
这第二项其实就是角动量守恒。可以这样证明:
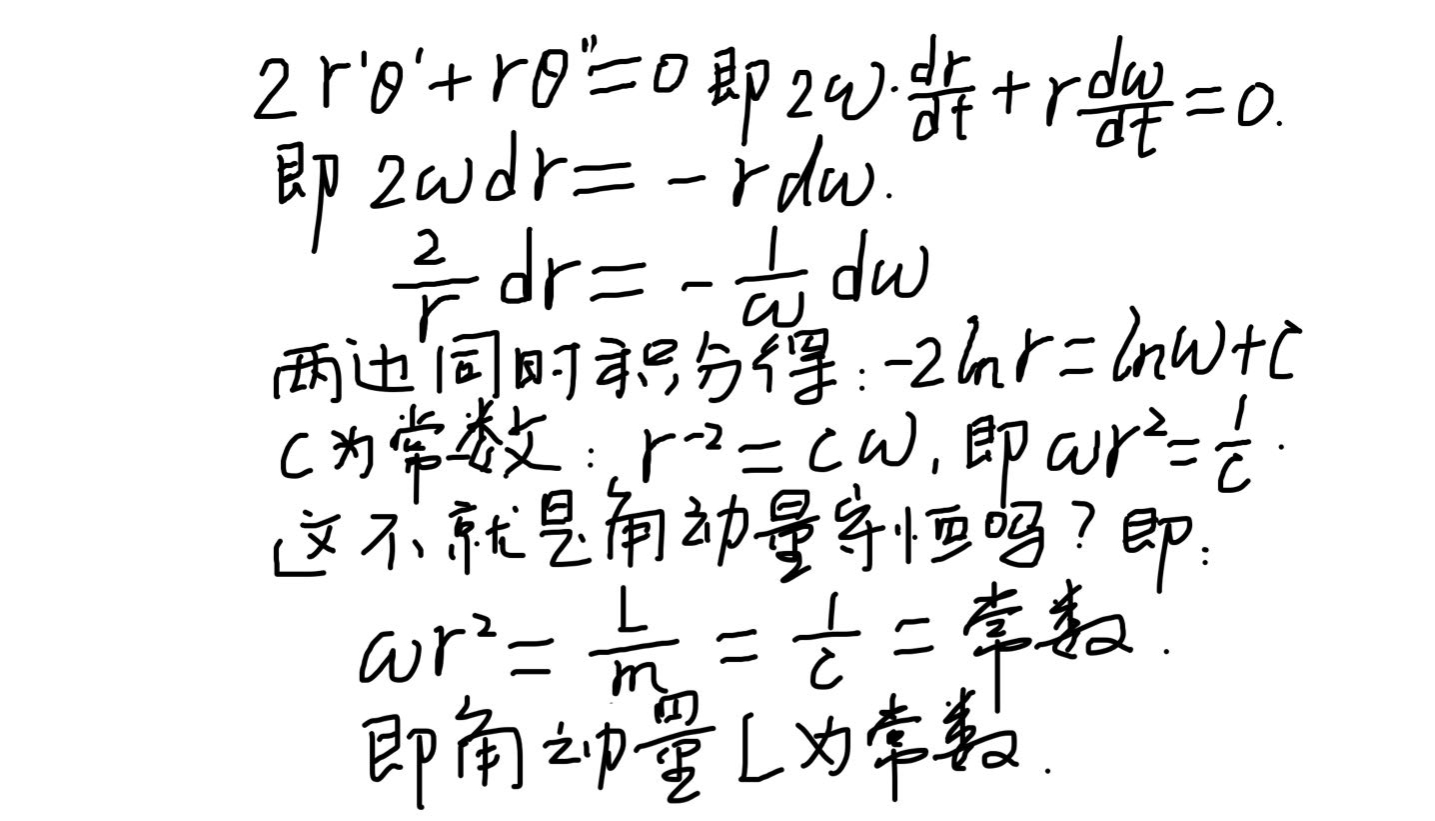
看懂这段始终要记住角速度ω等于极角θ对时间的一阶导数，ω和θ的方向都是横向的，描述矢径转动的。
接下来既然角动量守恒，那么行星轨迹必然为一个平面:
现在我们已经知道这个切向速度等于横向速度的时刻其实就是近日点或远日点
再次证明了行星公转运动的角动量是不变的
接下来我们要想办法求解前面写出的径向加速度的微分方程。
接下来就要将此式作为实质上的r关于t的微分方程换元成为r关于θ的微分方程，得出极坐标方程
京公网安备 11010802035086号