SimpleAI.

人工智能、机器学习、深度学习还是遥不可及？来这里看看吧~

从基本的概念、原理、公式，到用生动形象的例子去理解，到动手做实验去感知，到著名案例的学习，到用所学来实现自己的小而有趣的想法......我相信，一路看下来，我们可以感受到深度学习的无穷的乐趣，并有兴趣和激情继续钻研学习。

正所谓 Learning by teaching，写下一篇篇笔记的同时，我也收获了更多深刻的体会，希望大家可以和我一同进步，共同享受AI无穷的乐趣。

Logistic回归：最基础的神经网络

❝

个人认为理解并掌握这个logistic regression是学习神经网络和深度学习最重要的部分，也是最基础的部分，学完这个再去看浅层神经网络、深层神经网络，会发现后者就是logistic重复了若干次（当然一些细节会有不同，但是原理上一模一样）。

一、什么是logictic regression

下面的图是Andrew Ng提供的一个用logistic regression来识别主子的图片的算法结构示意图：

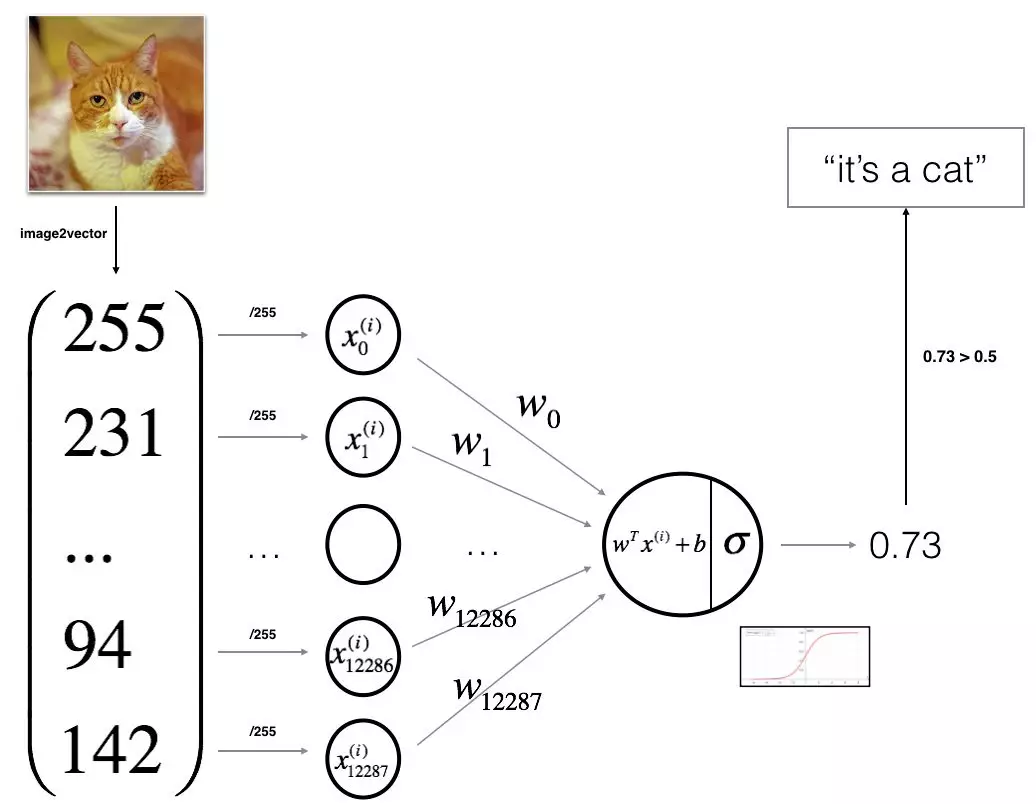
「左边」的「x0到x12287「是输入（input），我们称之为」特征（feather）」，常常用「列向量x(i)「来表示（这里的i代表第i个训练样本,下面在只讨论一个样本的时候，就暂时省略这个标记，免得看晕了-_-|||），在图片识别中，特征通常是图片的像素值，把所有的像素值排成一个序列就是输入特征，每一个特征都有自己的一个」权重（weight）」，就是图中连线上的「w0到w12287」，通常我们也把左右的权重组合成一个「列向量W」。

「中间的圆圈」，我们可以叫它一个神经元，它接收来自左边的输入并乘以相应的权重,再加上一个偏置项b（一个实数），所以最终接收的总输入为：

但是这个并不是最后的输出，就跟神经元一样，会有一个「激活函数（activation function）「来对输入进行处理，来决定是否输出或者输出多少。Logistic Regression的激活函数是」sigmoid函数」，介于0和1之间，中间的斜率比较大，两边的斜率很小并在远处趋于零。长这样（记住函数表达式）：

我们用来表示该神经元的输出，σ()函数代表sigmoid，则可知：

这个可以看做是我们这个小模型根据输入做出的一个预测，在最开始的图对应的案例中，就是根据图片的像素在预测图片是不是猫。与对应的，每一个样本x都有自己的一个真实标签，代表图片是猫，代表不是猫。我们希望模型输出的可以尽可能的接近真实标签，这样，这个模型就可以用来预测一个新图片是不是猫了。所以，我们的任务就是要找出一组W，b，使得我们的模型可以根据给定的，正确地预测。在此处，我们可以认为，只要算出的大于0.5，那么y'就更接近1，于是可以预测为“是猫”，反之则“不是猫”。

以上就是Logistic Regression的基本结构说明。

二、怎么学习W和b

前面其实提到过了，我们「需要学习到的W和b可以让模型的预测值y'与真实标签y尽可能地接近，也就是y'和y的差距尽量地缩小」。因此，我们可以定义一个「损失函数（Loss function）」，来衡量和y的差距：

实际上，这就是交叉熵损失函数，Cross-entropy loss。交叉熵衡量了两个不同分布之间的差距，在这里，即衡量我们预测出来的分布和正式分布之间的差距。

如何说明这个式子适合当损失函数呢？且看：

• 当y=1时，，要使L最小，则要最大，则=1；
• 当y=0时，，要使L最小，则要最小，则=0.

如此，便知符合我们对损失函数的期望，因此适合作为损失函数。

我们知道，x代表一组输入，相当于是一个样本的特征。但是我们训练一个模型会有很多很多的训练样本，也就是有很多很多的x，就是会有x(1)，x(2)，...，x(m) 共m个样本（m个列向量），它们可以写成一个X矩阵：

对应的我们也有m个标签，：

通过我们的模型计算出的也会有m个：

前面我们写的损失函数，只计算一个样本的损失。但我们需要考虑所有训练样本的损失，则总损失可以这样计算：

有了总体的损失函数，我们的学习任务就可以用一句话来表述：

“寻找w和b，使得损失函数最小化”

最小化。。。说起来简单做起来难，好在我们有计算机，可以帮我们进行大量重复地运算，于是在神经网络中，我们一般使用「梯度下降法（Gradient Decent）」：

这个方法通俗一点就是，先随机在曲线上找一个点，然后求出该点的斜率，也称为梯度，然后顺着这个梯度的方向往下走一步，到达一个新的点之后，重复以上步骤，直到到达最低点（或达到我们满足的某个条件）。如，对w进行梯度下降，则就是重复一下步骤（重复一次称为一个「迭代」）：

其中:=代表“用后面的值更新”，α代表「学习率（learning rate）」，dJ/dw就是J对w求偏导。

回到我们的Logistic Regression问题，就是要初始化（initializing）一组W和b，并给定一个学习率，指定要「迭代的次数」（就是你想让点往下面走多少步），然后每次迭代中求出w和b的梯度，并更新w和b。最终的W和b就是我们学习到的W和b，把W和b放进我们的模型中，就是我们学习到的模型，就可以用来进行预测了！

需要注意的是，这里我们使用的损失是全体训练样本的损失。实际上，使用全部样本的损失进行更新的话会太慢，但使用一个样本进行更新，误差就会很大。所以，我们更常用的是选择「一定大小的批次」（batch），然后计算一个batch内的损失，再进行参数更新。

总结一下：

• Logistic Regression模型：，记住使用的激活函数是sigmoid函数。
• 损失函数：衡量预测值与真实值的差距，越小越好。
• 我们一般对一个批次的样本求总损失，然后使用梯度下降法进行更新。
• 「训练模型的步骤」：
• 初始化W和b
• 指定learning rate和迭代次数
• 每次迭代，根据当前W和b计算对应的梯度（J对W，b的偏导数），然后更新W和b
• 迭代结束，学得W和b，带入模型进行预测，分别测试在训练集合测试集上的准确率，从而评价模型

就这么明明白白