前言
在头条创作了一个月左右的时间,收获了50+粉丝,很是开心,我会把数据结构与算法的文章更新到底,第一次看我文章的同仁如果觉得不错的话就关注一下我哦,你的支持就是我创作的动力。
一、什么是跳表
我们在之前介绍了十分优秀的二分查找算法,但是它只能作用于有序数组上,查找起来比较方便,但是数组中插入和删除元素是比较麻烦的;那么有没有办法让二分查找也能作用于有序链表上,从而达到查找、插入和删除元素都十分的快速呢?
对于普通的有序列表来说,当然不能实现我们的目标,如下查找的时间复杂度为O(n);

原始有序单链表
我们可以基于原始链表建立一个 索引层,比如每两个节点提取一个节点到索引层:
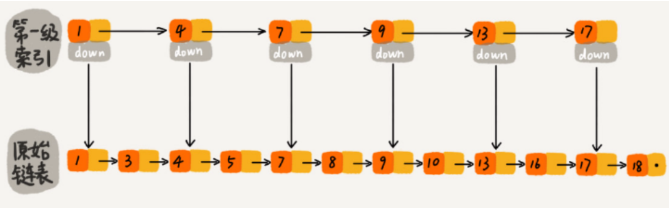
带一级索引的跳表
如此,两种数据结构我们查找元素16的比较次数分别为10次和8次,确实能提高查询速度;我们更近一步,再次建立第二级索引:
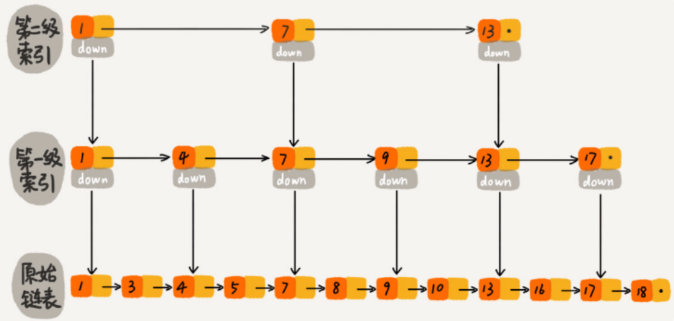
带二级索引的跳表 带二级索引的跳表
此时查找元素16比较的次数只需要比较7次即可;
如果在大数据量的有序链表中,我们建立很多层索引,使得最高层索引只有两个节点,那么就实现了类似二分查找的算法思想,此时这种数据结构就被成为跳表。
二、跳表性能分析
2.1 时间复杂度
假设有序链表总节点个数为n,我们建立索引时每两个节点提取一个索引节点;那么第一级索引共有n/2个节点;
第k级索引共有(n/2^k)个节点,假设k为最高级索引,为2个节点,那么2=(n/2^k),n=2(k+1),k=logn-1,如果原始链表也算进去的话,k=logn正好是整个数据结构的高度。
假设每一层需要遍历m个节点,那么时间复杂度就可以表示为O(mlogn),但是推断m是常量级别的,因此可以忽略,那么整个查找过程时间复杂度就是O(logn),竟然和二分查找是一样的高效!
2.2 空间复杂度
第一级索引需要n/2个节点,第二级需要n/2^2个节点,依次类推,第k级索引需要的节点个数为n/2^k,这正好是一个等比数列,等比数列求和的结果是n-2,所以空间复杂度为O(n),这是一个以空间换时间的策略;
我们可以每3个节点或者每4个节点往上提取一个索引节点,如此可以适当减少需要的额外空间,但是空间复杂度仍然为O(n);如果有序链表存储的是大对象,那么索引节点中无需存放整个大对象,只要存储对象的指针即可,所以此时空间复杂度就显得不那么重要了;
2.3 跳表的插入和删除
跳表因为是顺序链表,所以真正插入和删除的时间复杂度都是O(1),但是找到需要插入节点的位置或者找到待删除的节点时间复杂度为O(logn);
跳表在删除的时候,除了需要删除原始有序链表中的节点,还需要同步删除k级索引中的全部该索引节点;
跳表在插入元素式,极端情况下会导致两个索引节点中存在大量的原始节点,时间效率极有可能会退化为单链表的O(n),所以需要动态地平衡和更新k级索引节点;
三、跳表使用场景
redis在存储有序集合的时候就用到了跳表+散列表的数据结构,跳表和红黑树相比,插入、删除、查找的时间复杂度相同,但是跳表在按照区间查找时明显具有效率优势,而且跳表实现起来比红黑树要简单易懂,不容易出错。
红黑树等常用数据结构在程序语言中都是封装好的,我们想用的话直接拿来用即可,比如HashMap,但是跳表却没有对应的封装好的数据结构,想用的话开发者必须自己去实现。
四、代码实现跳表Skiplist以及优化
代码来源于极客时间《数据结构和算法之美》
Github地址:
https://github.com/wangzheng0822/algo(数据结构和算法必知必会的50个代码实现)
4.1 作者王争给出的跳表实现方式
/**
* 跳表的一种实现方法。
* 跳表中存储的是正整数,并且存储的是不重复的。
*
*/
public class SkipList {
private static final float SKIPLIST_P = 0.5f;
private static final int MAX_LEVEL = 16;
private int levelCount = 1;
private Node head = new Node(); // 带头链表
public Node find(int value) {
Node p = head;
for (int i = levelCount - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
p = p.forwards[i];
}
}
if (p.forwards[0] != null && p.forwards[0].data == value) {
return p.forwards[0];
} else {
return null;
}
}
public void insert(int value) {
int level = randomLevel();
Node newNode = new Node();
newNode.data = value;
newNode.maxLevel = level;
Node update[] = new Node[level];
for (int i = 0; i < level; ++i) {
update[i] = head;
}
// record every level largest value which smaller than insert value in update[]
Node p = head;
for (int i = level - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
p = p.forwards[i];
}
update[i] = p;// use update save node in search path
}
// in search path node next node become new node forwords(next)
for (int i = 0; i < level; ++i) {
newNode.forwards[i] = update[i].forwards[i];
update[i].forwards[i] = newNode;
}
// update node hight
if (levelCount < level) levelCount = level;
}
public void delete(int value) {
Node[] update = new Node[levelCount];
Node p = head;
for (int i = levelCount - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
p = p.forwards[i];
}
update[i] = p;
}
if (p.forwards[0] != null && p.forwards[0].data == value) {
for (int i = levelCount - 1; i >= 0; --i) {
if (update[i].forwards[i] != null && update[i].forwards[i].data == value) {
update[i].forwards[i] = update[i].forwards[i].forwards[i];
}
}
}
while (levelCount>1&&head.forwards[levelCount]==null){
levelCount--;
}
}
// 理论来讲,一级索引中元素个数应该占原始数据的 50%,二级索引中元素个数占 25%,三级索引12.5% ,一直到最顶层。
// 因为这里每一层的晋升概率是 50%。对于每一个新插入的节点,都需要调用 randomLevel 生成一个合理的层数。
// 该 randomLevel 方法会随机生成 1~MAX_LEVEL 之间的数,且 :
// 50%的概率返回 1
// 25%的概率返回 2
// 12.5%的概率返回 3 ...
private int randomLevel() {
int level = 1;
while (Math.random() < SKIPLIST_P && level < MAX_LEVEL)
level += 1;
return level;
}
public void printAll() {
Node p = head;
while (p.forwards[0] != null) {
System.out.print(p.forwards[0] + " ");
p = p.forwards[0];
}
System.out.println();
}
public class Node {
private int data = -1;
private Node forwards[] = new Node[MAX_LEVEL];
private int maxLevel = 0;
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
builder.Append("{ data: ");
builder.append(data);
builder.append("; levels: ");
builder.append(maxLevel);
builder.append(" }");
return builder.toString();
}
}
}4.2 作者ldb基于王争的代码给出的优化
import JAVA.util.Random;
/**
* 1,跳表的一种实现方法,用于练习。跳表中存储的是正整数,并且存储的是不重复的。
* 2,本类是参考作者zheng ,自己学习,优化了添加方法
* 3,看完这个,我觉得再看ConcurrentSkipListMap 源码,会有很大收获
*/
public class SkipList2 {
private static final int MAX_LEVEL = 16;
private int levelCount = 1;
/**
* 带头链表
*/
private Node head = new Node(MAX_LEVEL);
private Random r = new Random();
public Node find(int value) {
Node p = head;
// 从最大层开始查找,找到前一节点,通过--i,移动到下层再开始查找
for (int i = levelCount - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
// 找到前一节点
p = p.forwards[i];
}
}
if (p.forwards[0] != null && p.forwards[0].data == value) {
return p.forwards[0];
} else {
return null;
}
}
/**
* 优化了作者zheng的插入方法
*
* @param value 值
*/
public void insert(int value) {
int level = head.forwards[0] == null ? 1 : randomLevel();
// 每次只增加一层,如果条件满足
if (level > levelCount) {
level = ++levelCount;
}
Node newNode = new Node(level);
newNode.data = value;
Node update[] = new Node[level];
for (int i = 0; i < level; ++i) {
update[i] = head;
}
Node p = head;
// 从最大层开始查找,找到前一节点,通过--i,移动到下层再开始查找
for (int i = levelCount - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
// 找到前一节点
p = p.forwards[i];
}
// levelCount 会 > level,所以加上判断
if (level > i) {
update[i] = p;
}
}
for (int i = 0; i < level; ++i) {
newNode.forwards[i] = update[i].forwards[i];
update[i].forwards[i] = newNode;
}
}
/**
* 优化了作者zheng的插入方法2
*
* @param value 值
*/
public void insert2(int value) {
int level = head.forwards[0] == null ? 1 : randomLevel();
// 每次只增加一层,如果条件满足
if (level > levelCount) {
level = ++levelCount;
}
Node newNode = new Node(level);
newNode.data = value;
Node p = head;
// 从最大层开始查找,找到前一节点,通过--i,移动到下层再开始查找
for (int i = levelCount - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
// 找到前一节点
p = p.forwards[i];
}
// levelCount 会 > level,所以加上判断
if (level > i) {
if (p.forwards[i] == null) {
p.forwards[i] = newNode;
} else {
Node next = p.forwards[i];
p.forwards[i] = newNode;
newNode.forwards[i] = next;
}
}
}
}
/**
* 作者zheng的插入方法,未优化前,优化后参见上面insert()
*
* @param value
* @param level 0 表示随机层数,不为0,表示指定层数,指定层数
* 可以让每次打印结果不变动,这里是为了便于学习理解
*/
public void insert(int value, int level) {
// 随机一个层数
if (level == 0) {
level = randomLevel();
}
// 创建新节点
Node newNode = new Node(level);
newNode.data = value;
// 表示从最大层到低层,都要有节点数据
newNode.maxLevel = level;
// 记录要更新的层数,表示新节点要更新到哪几层
Node update[] = new Node[level];
for (int i = 0; i < level; ++i) {
update[i] = head;
}
/**
*
* 1,说明:层是从下到上的,这里最下层编号是0,最上层编号是15
* 2,这里没有从已有数据最大层(编号最大)开始找,(而是随机层的最大层)导致有些问题。
* 如果数据量为1亿,随机level=1 ,那么插入时间复杂度为O(n)
*/
Node p = head;
for (int i = level - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
p = p.forwards[i];
}
// 这里update[i]表示当前层节点的前一节点,因为要找到前一节点,才好插入数据
update[i] = p;
}
// 将每一层节点和后面节点关联
for (int i = 0; i < level; ++i) {
// 记录当前层节点后面节点指针
newNode.forwards[i] = update[i].forwards[i];
// 前一个节点的指针,指向当前节点
update[i].forwards[i] = newNode;
}
// 更新层高
if (levelCount < level) levelCount = level;
}
public void delete(int value) {
Node[] update = new Node[levelCount];
Node p = head;
for (int i = levelCount - 1; i >= 0; --i) {
while (p.forwards[i] != null && p.forwards[i].data < value) {
p = p.forwards[i];
}
update[i] = p;
}
if (p.forwards[0] != null && p.forwards[0].data == value) {
for (int i = levelCount - 1; i >= 0; --i) {
if (update[i].forwards[i] != null && update[i].forwards[i].data == value) {
update[i].forwards[i] = update[i].forwards[i].forwards[i];
}
}
}
}
/**
* 随机 level 次,如果是奇数层数 +1,防止伪随机
*
* @return
*/
private int randomLevel() {
int level = 1;
for (int i = 1; i < MAX_LEVEL; ++i) {
if (r.nextInt() % 2 == 1) {
level++;
}
}
return level;
}
/**
* 打印每个节点数据和最大层数
*/
public void printAll() {
Node p = head;
while (p.forwards[0] != null) {
System.out.print(p.forwards[0] + " ");
p = p.forwards[0];
}
System.out.println();
}
/**
* 打印所有数据
*/
public void printAll_beautiful() {
Node p = head;
Node[] c = p.forwards;
Node[] d = c;
int maxLevel = c.length;
for (int i = maxLevel - 1; i >= 0; i--) {
do {
System.out.print((d[i] != null ? d[i].data : null) + ":" + i + "-------");
} while (d[i] != null && (d = d[i].forwards)[i] != null);
System.out.println();
d = c;
}
}
/**
* 跳表的节点,每个节点记录了当前节点数据和所在层数数据
*/
public class Node {
private int data = -1;
/**
* 表示当前节点位置的下一个节点所有层的数据,从上层切换到下层,就是数组下标-1,
* forwards[3]表示当前节点在第三层的下一个节点。
*/
private Node forwards[];
/**
* 这个值其实可以不用,看优化insert()
*/
private int maxLevel = 0;
public Node(int level) {
forwards = new Node[level];
}
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
builder.append("{ data: ");
builder.append(data);
builder.append("; levels: ");
builder.append(maxLevel);
builder.append(" }");
return builder.toString();
}
}
public static void mAIn(String[] args) {
SkipList2 list = new SkipList2();
list.insert(1, 3);
list.insert(2, 3);
list.insert(3, 2);
list.insert(4, 4);
list.insert(5, 10);
list.insert(6, 4);
list.insert(8, 5);
list.insert(7, 4);
list.printAll_beautiful();
list.printAll();
/**
* 结果如下:
* null:15-------
* null:14-------
* null:13-------
* null:12-------
* null:11-------
* null:10-------
* 5:9-------
* 5:8-------
* 5:7-------
* 5:6-------
* 5:5-------
* 5:4-------
* 8:4-------
* 4:3-------5:3-------6:3-------7:3-------8:3-------
* 1:2-------2:2------- 4:2-------5:2-------6:2-------7:2-------8:2-------
* 1:1-------2:1-------3:1-------4:1-------5:1-------6:1-------7:1-------8:1-------
* 1:0-------2:0-------3:0-------4:0-------5:0-------6:0-------7:0-------8:0-------
* { data: 1; levels: 3 } { data: 2; levels: 3 } { data: 3; levels: 2 } { data: 4; levels: 4 }
* { data: 5; levels: 10 } { data: 6; levels: 4 } { data: 7; levels: 4 } { data: 8; levels: 5 }
*/
// 优化后insert()
SkipList2 list2 = new SkipList2();
list2.insert2(1);
list2.insert2(2);
list2.insert2(6);
list2.insert2(7);
list2.insert2(8);
list2.insert2(3);
list2.insert2(4);
list2.insert2(5);
System.out.println();
list2.printAll_beautiful();
}
}




























