
关注国产芯片事业的你,一定有很多困惑,能让大国科技举步维艰的技术,到底是有多难?
其实,芯片这个东西,说难是真难,就拿5nm光刻机来说,10多万个零部件组成,一个一个数一遍,可能大部分我们现在都不能生产。
可是,芯片说简单也简单,从原理上来说,只要你有一定的知识基础,都能搞清楚。在这一点上还确实是“科技无国界”。至少到现在,相关的书籍、论文等知识都是能够公开获取到的,差的主要就是产业经验和技术实力。
今天,我就和大家一起看看芯片到底有多简单,本文的目标是科普一些基本数学知识,然后设计一个最简单的芯片!
芯片,作为最重要的半导体产品,实现了特定功能。比如电脑CPU实现了计算、显示、读写内存硬盘数据、接受鼠标键盘输入等等丰富的功能。
那大家有没有想过,芯片的基础是什么?
可能有人马上会想到硅,硅作为半导体材料是芯片的基础。可是喝水的玻璃杯也有硅呀,它就不值钱,所以硅不是根本基础。芯片为什么要用硅?是因为要在硅上面制造集成电路!硅的特点是能在很小的面积上集成大量的电路器件。
这么说芯片的基础是电路?电路有很多种,家里的灯泡和开关也组成一个电路,这和芯片没啥关系。芯片用到的是逻辑电路。
再试一次,芯片的基础是逻辑电路?呃,已经很接近了,但是还不是,逻辑电路是做逻辑运算的,逻辑运算也叫布尔代数运算。
所以,芯片的根本基础是数学!更具体的说是布尔代数!
这个结论一点儿也不奇怪,大家都知道物理学的基础是数学,就连伟大的物理学家牛顿都和阿基米德、高斯一起并称世界三大数学家。
了解最基本的布尔代数,你就会知道机器是怎么运算,也就明白了芯片要怎样设计。
接下来我就介绍一下二进制和布尔代数,下面的内容争取让小朋友都能明白。
为什么能让小朋友都明白呢?因为数学家布尔本人,就没上过大学,靠自学成才,并在19岁开办了一所小学,经营了10多年。他认为自己最主要的职业是教师,他的愿望是帮孩子们找到理解和掌握复杂规律的方法。
布尔代数的起源,是希望用数学表达人的逻辑思维。
其中和计算机相关的是几个重要的布尔运算:
1、与 运算
举个例子:我喜欢吃烤羊肉串
我们让A代表烧烤,B代表羊肉串。
则上面的表达变为了:
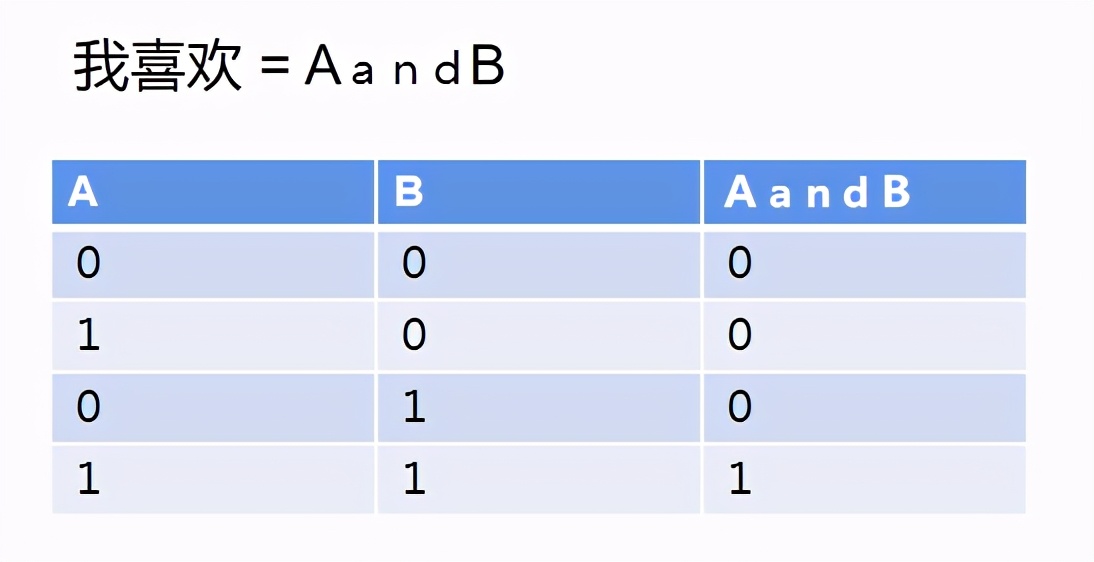
A和B都是真,做运算的结果才是真。比如,烤牛肉串,就是A=1,B=0,AandB=0。所以我不喜欢烤牛肉串。
2、或 运算
举个例子:我喜欢吃烧烤或是火锅。
我们让A代表烧烤,B代表火锅。
则上面的表达变成了:
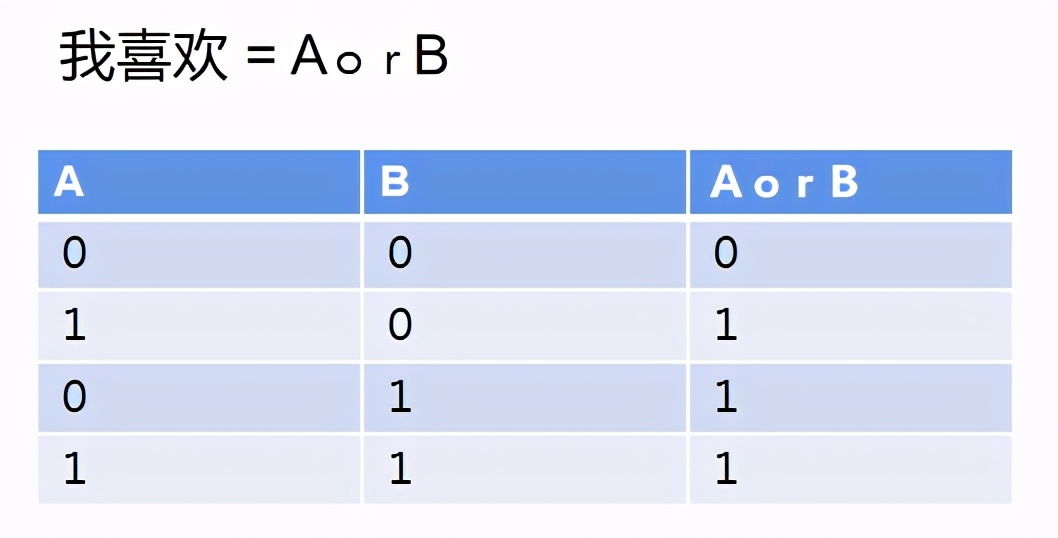
不管是烧烤还是火锅,只要有一个我就吃,当然两样都来更好!
3、非 运算
举个例子:我不喜欢吃辣。
我们让A代表辣。
则上面的表达变成了:
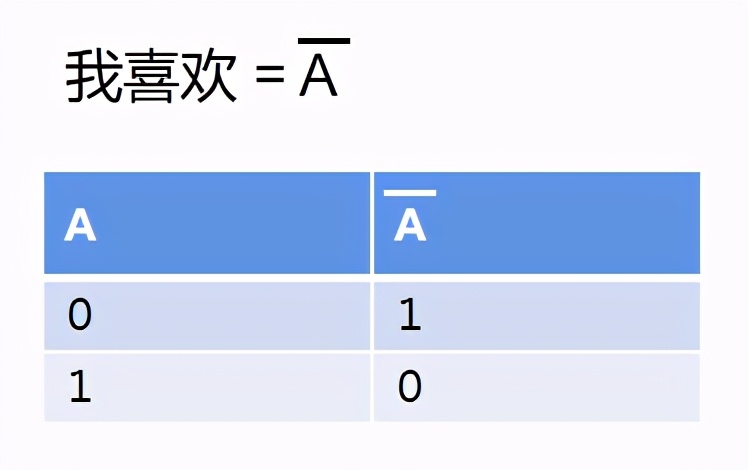
4、异或 运算
举个例子:我最喜欢吃烧烤和冰激凌,但是一起吃会拉肚子。
我们让A代表烧烤,B代表冰激凌。
则上面的表达变成了:
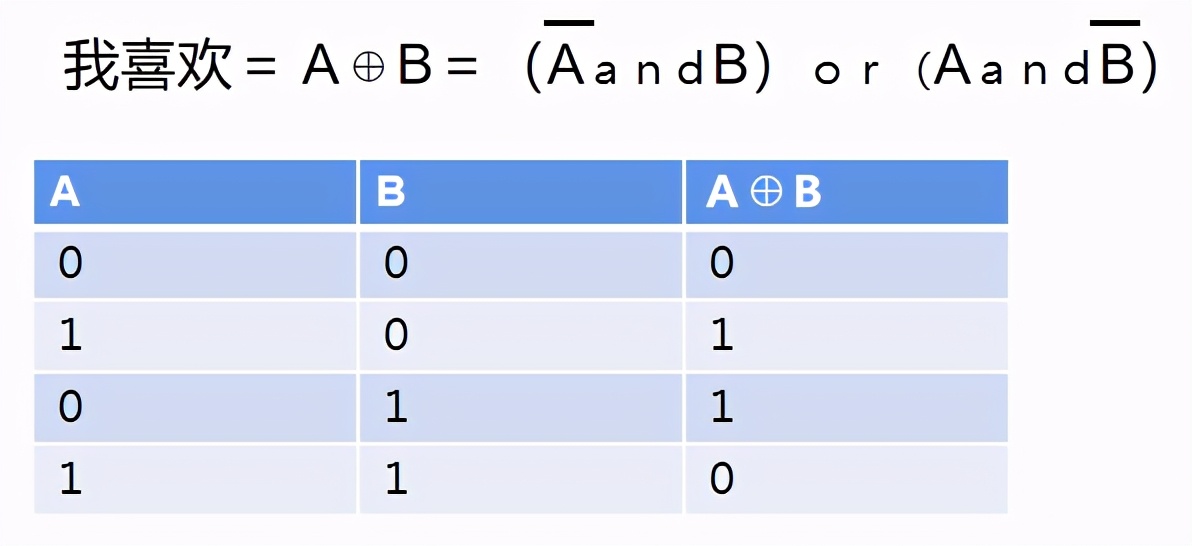
理解这个运算可能有点儿难,啥意思呢?就是A和B不能一样,没有烧烤没有冰激凌肯定不行,可是一起来也承受不了!
除了上面4种布尔运算,还有与非、或非、异或非运算。从异或运算可以看出,全部的运算都可以由与、或、非运算结合产生。
咱们接着讲二进制运算。
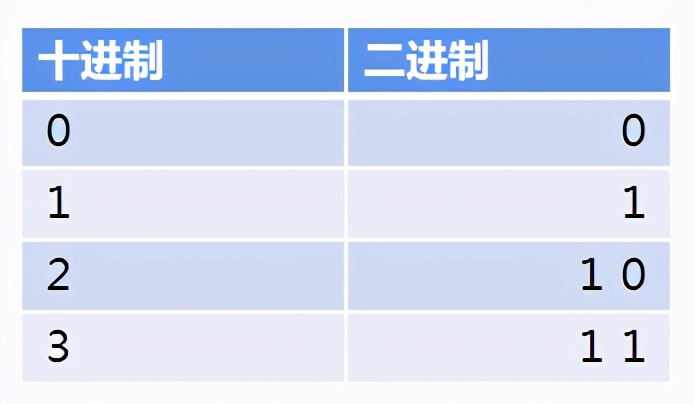
二进制就是用0、1表示一切数字,每一位上只能是0和1,到了2就要进位。
比如,十进制的2,用二进制表示就得进位了,变成两位数10,而十进制3就是11。
二进制是德国数学家莱布尼茨在300多年前发明的,那个时候连计算机的影子还没有,到底莱布尼茨为啥要发明一个当时根本没用的二进制,说实话没人能搞清楚。
说起二进制,不得不说一下我国的八卦,不是到处乱讲的那种娱乐圈八卦,而是真正的八卦。
八卦讲究的是两仪生四象,四象生八卦:

看到没有,很多人认为八卦就是二进制的先驱。两仪是阴阳,也就是0和1,四象是二进制两位数,八卦是二进制三位数,而伏羲64卦就是二进制的六位数:
貌似道理还真是一样,咱们的老祖先当时基于什么发明的八卦,说实话这也搞不清楚。
可有人却翻出了当时莱布尼茨和一位在北京生活的传教士的信,来试图证明莱布尼茨发明二进制是受了中国八卦的启发,而且很多人都信了这个说法。
实际的过程是这样的:当时莱布尼茨给这位传教士写信,希望他向康熙皇帝介绍二进制,这个传教士一看,这不就是中国的八卦么,给莱布尼茨回信说了八卦的情况。然后莱布尼茨写了一篇文章论述二进制在中国的实际应用。
莱布尼茨到底受没受八卦启发,都是猜测,就算莱布尼茨受了八卦的启发,那又怎样?在莱布尼茨发明二进制的时候,我们的康熙大帝正在打吴三桂呢,我们的现代文明还没有开化。
所以,关于八卦和二进制的事,我们就当它是八卦好了,咱们接着说二进制计算。
假设有两个一位的二进制数要相加,那么会有四种可能:
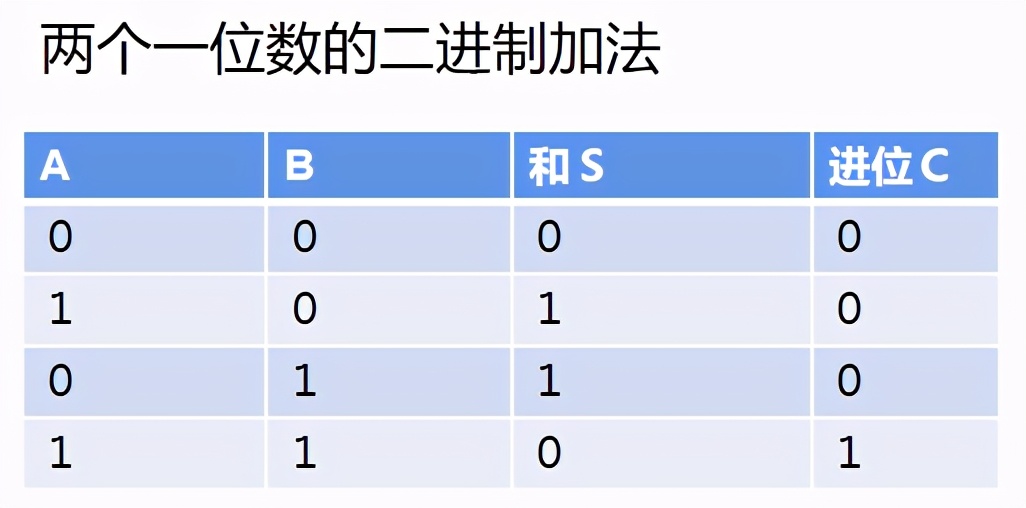
前三种情况不需要进位,后一种情况和S是一个两位二进制数,所以需要进位,我们单独设置一个进位标识C。
大家发现没有,二进制的加法和上面介绍的布尔运算是一样的:
我们用布尔运算符做个逻辑图,就是这样的:
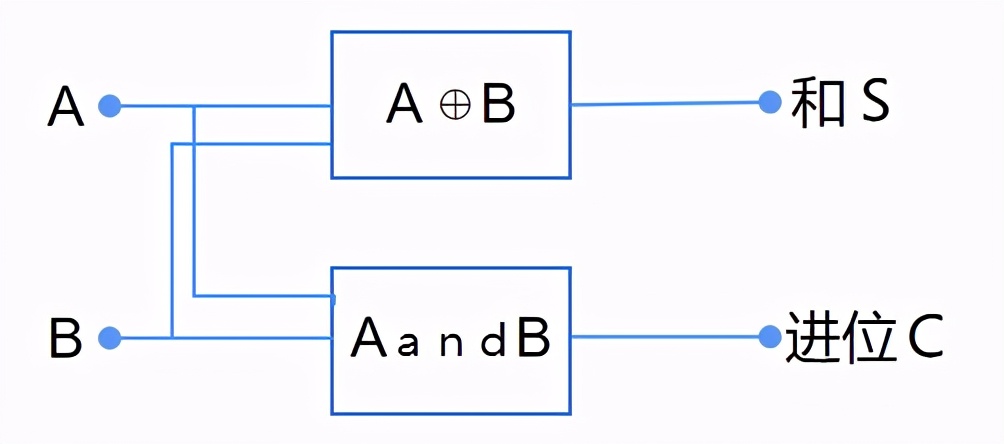
上面就是一个用布尔运算符表示的半加器,可以进一步表示如下:
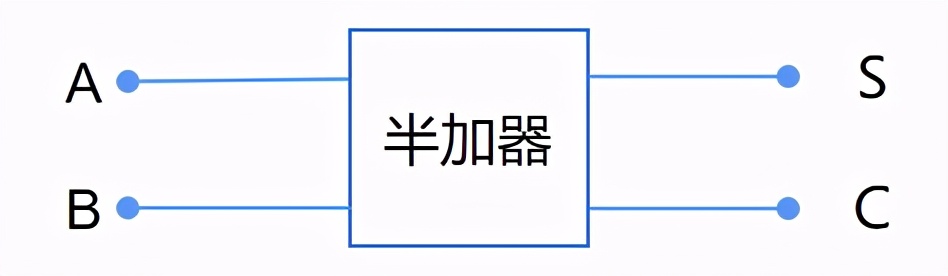
为什么叫半加器呢?这是因为计算A+B的时候,没有考虑上一位有没有进位的情况,所以这个半加器只能计算二进制数最末一位上的加法。
如果A和B不是末位上的数,那就要考虑前一位的计算结果有没有进位(Cin是上一位的进位标识,Cout是当前位计算完向上一位的进位情况),会有8种情况:
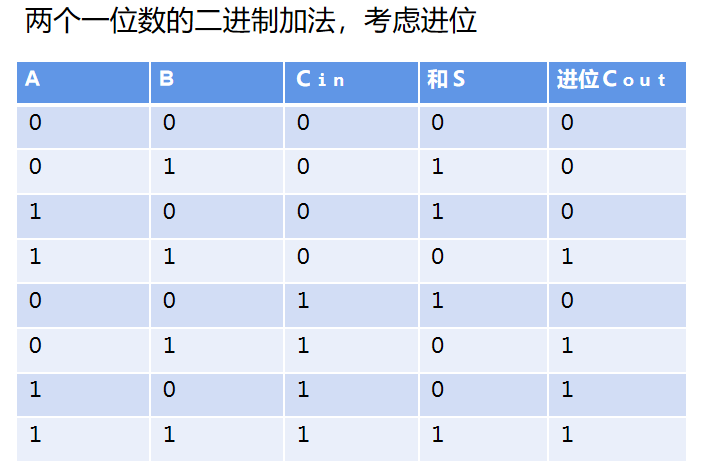
这个过程可以通过2个半加器和一个或运算来实现:
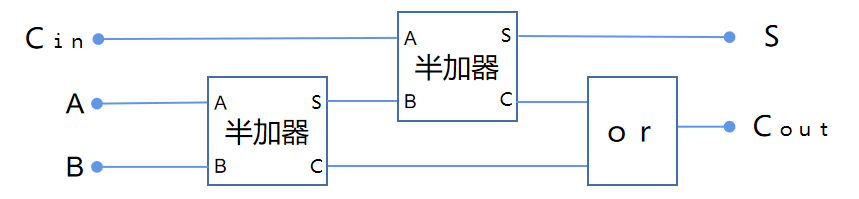
这就是全加器:
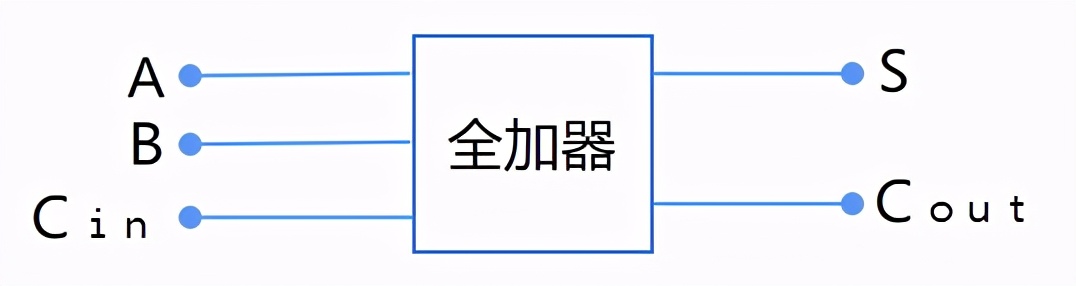
看,我们只用布尔代数的四个运算符,就实现了一位二进制数的加法。
其实,我们只用了三个运算符,因为异或运算可以画成与、或、非运算的组合,当然这样太麻烦。
全加器也是一样,如果我们不怕麻烦,可以细致的画成异或、与、或运算的组合。
大家看吧,关于计算机的数学也不难。
接下来最神奇的要来了,我们要用刚刚学到的布尔代数知识,设计一个最简单的芯片。
这是一个能够进行八位二进制数加法的加法器。
这还是有一些挑战的,这个加法器,如果做出来也算是一个最简单的芯片,真的是芯片哦!
这个加法器的输入是2个八位二进制数:
一个用A表示,八位分别是A[0],......,A[7];
另一个用B表示,八位分别是B[0],......,B[7];
还有一个输入是进位标识Cin,如果这个加法器单独使用时,这个输入始终置0。
输出是S,八位分别是S[0],......,S[7];
输出进位标识是Cout。
下面请大家看看,这个加法器到底是什么样子:
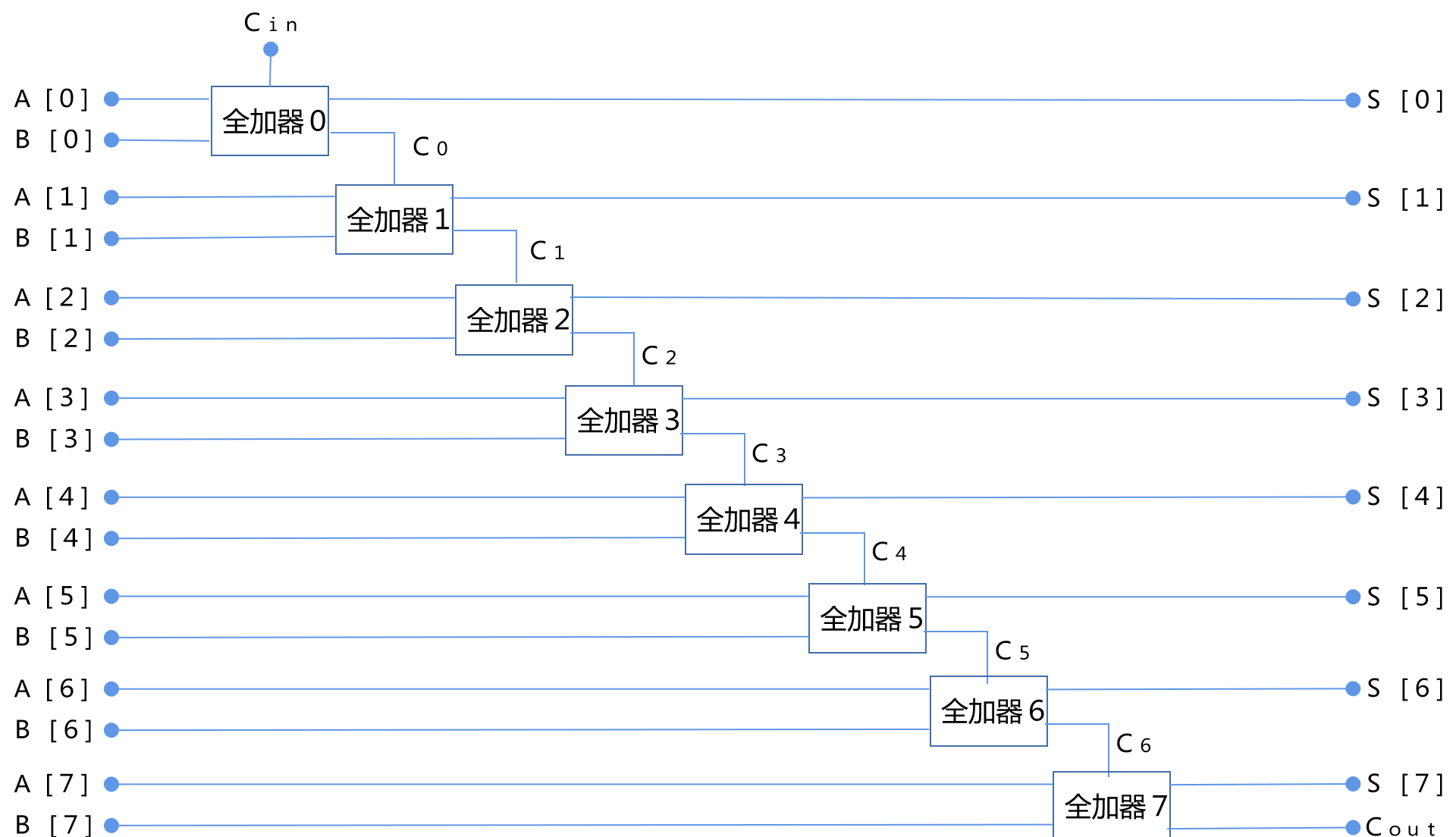
这就是一个用8个全加器构成的八位二进制加法器,神奇不神奇?
我们没有添加任何其他的东西,就是刚刚学过的全加器,如果大家有兴趣,可以把每个全加器用2个半加器和一个或运算符展开。
进一步可以再把每个半加器用异或运算符和与运算符展开,不知道哪位读者有兴趣,反正用手画,我是会崩溃的。
而这一切,在芯片设计的时候,都是由EDA软件来完成。
到此,我们已经在逻辑上设计了一个功能最简单的八位二进制加法芯片。
为什么要说是逻辑上呢?因为到目前为止,我们还没有用到任何电路知识。所涉及的全部是布尔代数知识,所以这个芯片是逻辑上可行,但是还无法制造。
那怎么做出实际能用的芯片呢?
首先我们需要有和上面布尔运算符对应的电子元件,实现同样的功能。然后按照设计把这些元件连接起来。这样就有了实际的电路,这种电路就叫门电路。实现了上面布尔运算的元件就叫门元件。
最终,我们要在硅片上面制作出这种门元件,这样就在硅片上面实现了门电路,也就是集成电路。
最后,再把这个集成电路切割下来,把输入输出引脚做好,然后封装,一个完整的芯片就产生了!
所有这些后续的工作,我都会在接下来的文章一点儿一点儿和大家一起学习!
如果您对我的文章感兴趣,欢迎关注我!
谢谢!