
学过编程的小伙伴们大多数都知道栈和队列这两种数据结构,这两个词我相信对大家来说并不陌生。栈和队列是一种特殊的线性结构,是咱们根据编码的需求衍生出来的两种逻辑上的数据结构,在这篇文章中,我们将详细的讲解一下栈这种数据结构,至于队列,咱们放在下一篇文章细讲。
栈的核心特点是先进后出,咱们生活中,类似的例子比比皆是,像蒸包子这个过程,我们总是一层一层的放入蒸笼,靠下层的包子总是先放入的,但是蒸熟过后,我们又总是从最上层开始一层一层取出的,这个时候我相信不会有人这么傻,蒸熟过后从下层一层一层取。此外呢,在咱们JAVA中,局部变量和方法调用的过程都是存储在栈内存的,像咱们的方法调用,递归调用,都是使用了栈这种先进后出的思想。比如A方法中调用B方法,B方法中又调用C方法。我们运行A方法后,总是会先让B方法执行,B方法执行时,又会优先让C方法执行,直到C方法执行结束后,返回给它的调用者B时,我们的B才会继续执行,B结束过后,返回给调用者A,A才会得以继续执行。在此过程中,我们方法的调用顺序为A->B->C,但是执行结束顺序则为C->B->A,刚好符合咱们栈先进后出的思想。
接下来了,我们针对栈这种数据结构,进行一个详细的讲解。
一、什么是栈?
栈是一种数据结构,是一种先进后出的特殊线性表,栈主要由两个指针组成,一部分叫做栈底,主要用来确定咱们栈的起始位置,对栈底来说,并不能操作数据。另一部分叫做栈顶,主要用于操作数据,像咱们栈的新增和删除都是在栈顶完成的。而对栈的新增操作,我们叫作入栈,而对栈的删除操作,我们叫作出栈或者弹栈。下面我们来看一下栈的内存图:
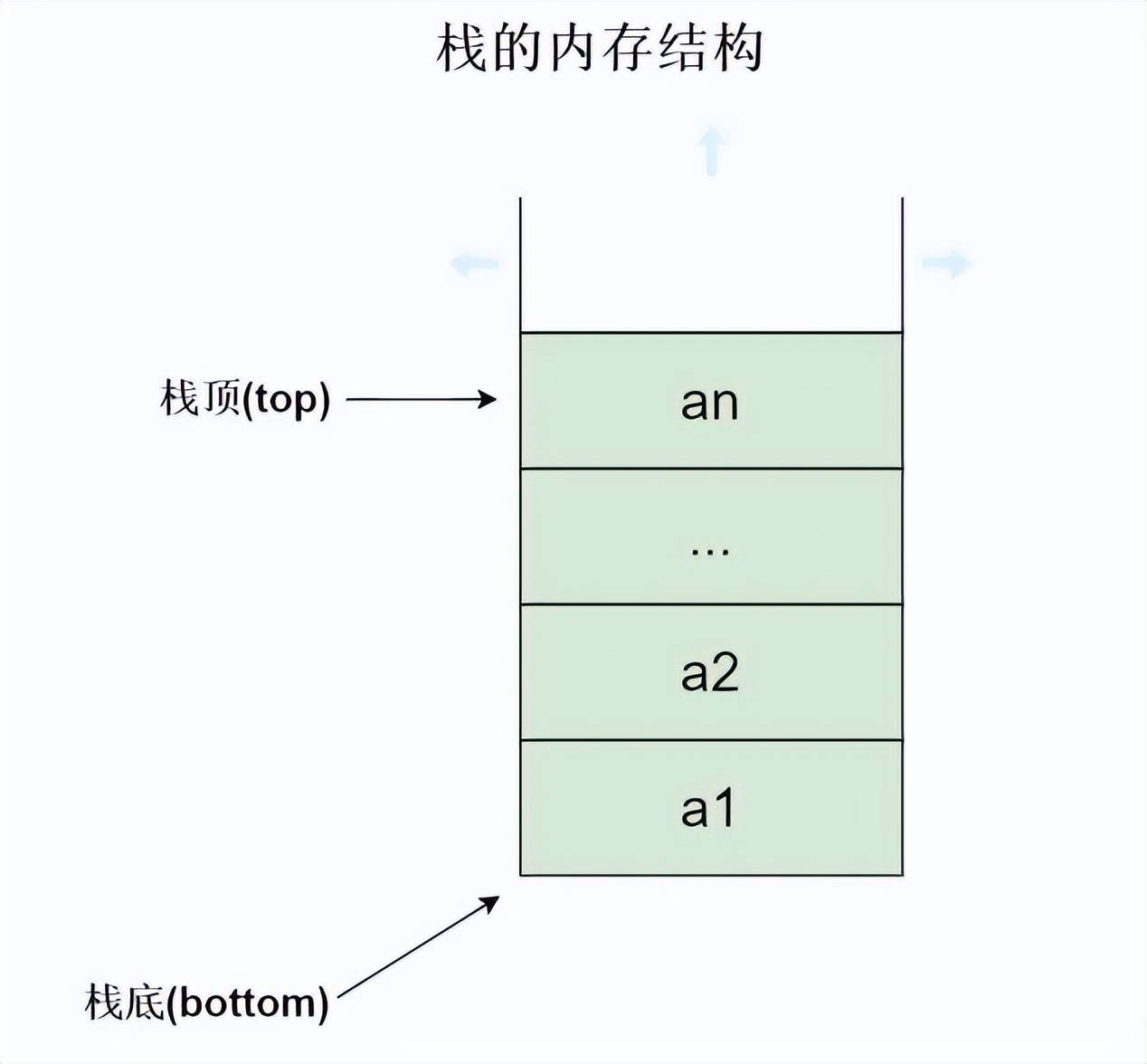
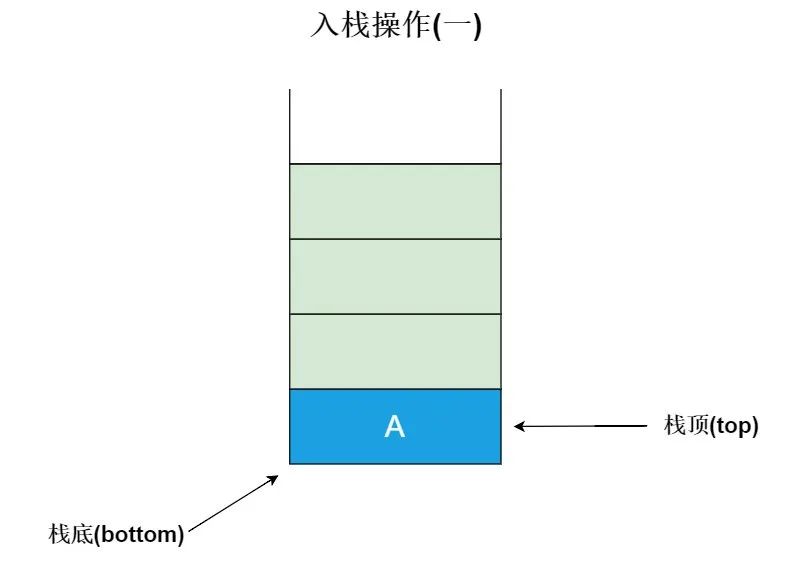
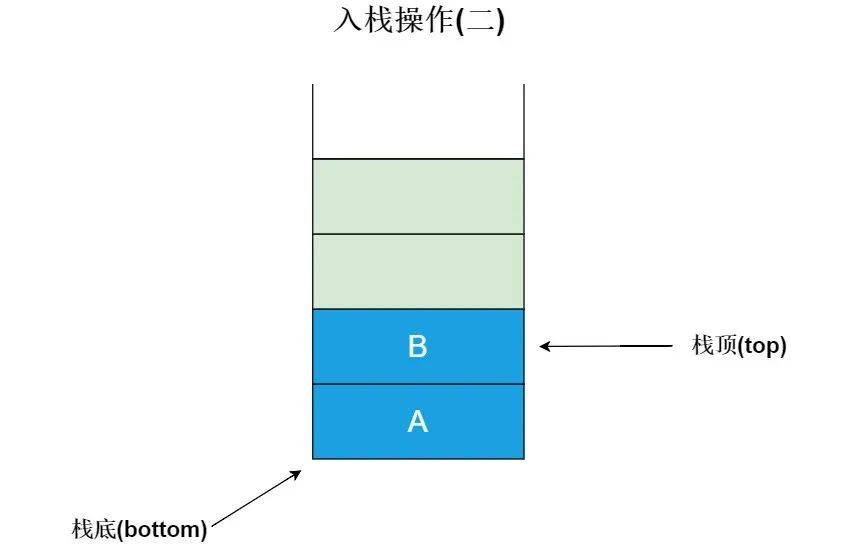
入栈:向栈中添加元素的过程,叫做入栈,每次入栈时,栈底指针保持不动,只需要移动栈顶指针即可。如下图所示:
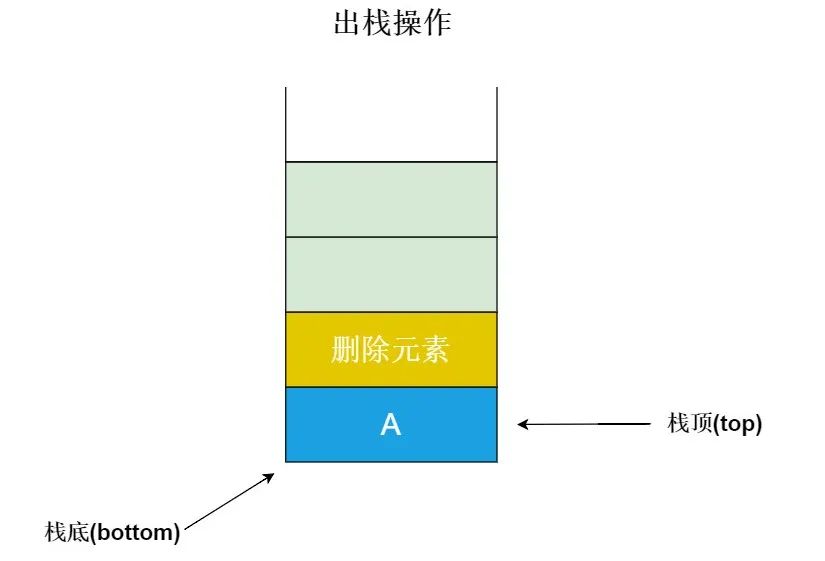
出栈(弹栈):向栈中删除元素的过程,叫做出栈或者弹栈,每次出栈时,栈底指针保持不动,只需要移动栈顶指针即可。如下图所示:
二、栈的实现
下面我们用最流行的Java语言完成栈的实现,咱们实现方式分为两种,第一种基于数组,第二种基于链表。如果对链表这种数据结构不熟悉的小伙伴,可以看看我之前写过的链表,在之前有专门且详细的讲解。
2.1数组实现栈
2.1.1 栈的抽象父类
因为咱们是通过两种方式实现栈,所以将一些公共的成员提取到咱们Stack抽象类中。在Stack类中,我们定义了一个属性size,用来表示咱们栈中实际的有效元素个数,isFull()方法主要用于判断咱们的栈是否满,同理isEmpty()方法用于判断咱们的栈是否存在元素,push()为入栈操作,pop()为出栈或者弹栈操作,show()方法主要查看咱们栈的存储情况。
package com.ignoarance.stack;
/**
* @ClassName Stack
* @Description 栈的父类
* @Author ignorance
* @Version 1.0
* bottom表示栈底指针,用于确定咱们栈的开始,top表示栈顶指针,用于完成咱们栈主要的操作。
**/
public abstract class Stack<T> {
private int size;//栈的实际有效元素个数
public int getSize() {
return size;
}
public void setSize(int size) {
this.size = size;
}
/**
* 判断当前栈是否满
* 是返回true,否返回false
* @return
*/
public abstract boolean isFull();
/**
* 判断当前栈是否空
* 是返回true,否返回false
* @return
*/
public abstract boolean isEmpty();
/**
* 入栈核心方法
*/
public abstract void push(T element);
/**
* 出栈方法
* 并返回出栈元素
* @return
*/
public abstract T pop();
/**
* 遍历方法
*/
public abstract void show();
}
2.1.2 ArrayStack实现类
ArrayStack主要为数组实现栈的核心类,在该类中,我们定义elementData数组主要用于存放元素,maxSize表示底层数组的初始化长度,也就是栈能够存放元素的数量,bottom和top分别表示栈底和栈顶。在构造器中,我们初始化底层数组长度,以及bottom和top的初始值都为-1。那么现在咱们的栈结构示意图如下:
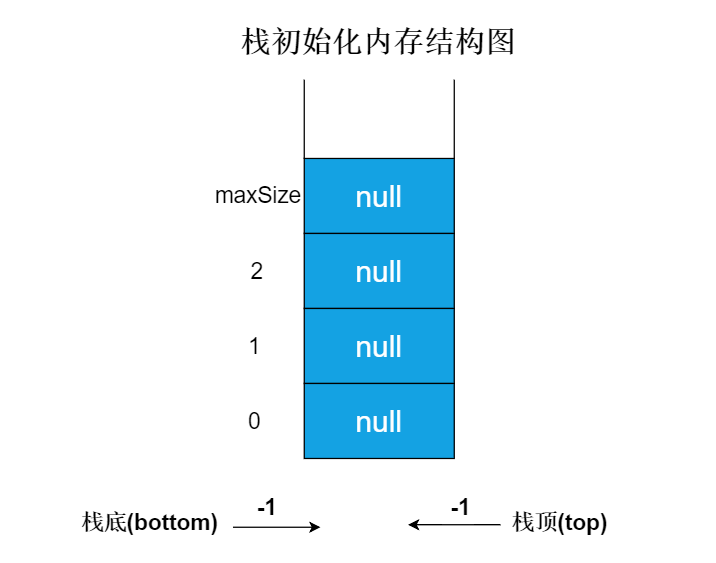
核心代码如下:
package com.ignoarance.stack;
/**
* @ClassName ArrayStack
* @Description 数组实现栈核心类
* @Author ignorance
* @Version 1.0
**/
public class ArrayStack<T> extends Stack<T> {
private T[] elementData;//栈的核心存储结构【数组】
private final int maxSize;//数组最大长度
private int bottom;//栈底指针
private int top;//栈顶指针
public ArrayStack(T[] elementData) {
this.elementData = elementData;//初始化底层数组
this.maxSize = elementData.length;
this.bottom = -1;//将栈底索引置为-1
this.top = -1;//将栈顶索引置为-1
}
@Override
public boolean isFull() {
return false;
}
@Override
public boolean isEmpty() {
return false;
}
@Override
public void push(T element) {
}
@Override
public T pop() {
return null;
}
@Override
public void show() {
}
}
2.1.3 判断栈满和栈空
下面我们完成isFull()这个方法,什么时候栈满呢?也就是咱们栈中不能再添加元素了,咱们是通过数组完成栈结构的,又因为咱们的数组的最大索引为maxSize-1,所以当咱们的top移动到top=maxSize-1时也就表示咱们的栈已满。如下图所示:
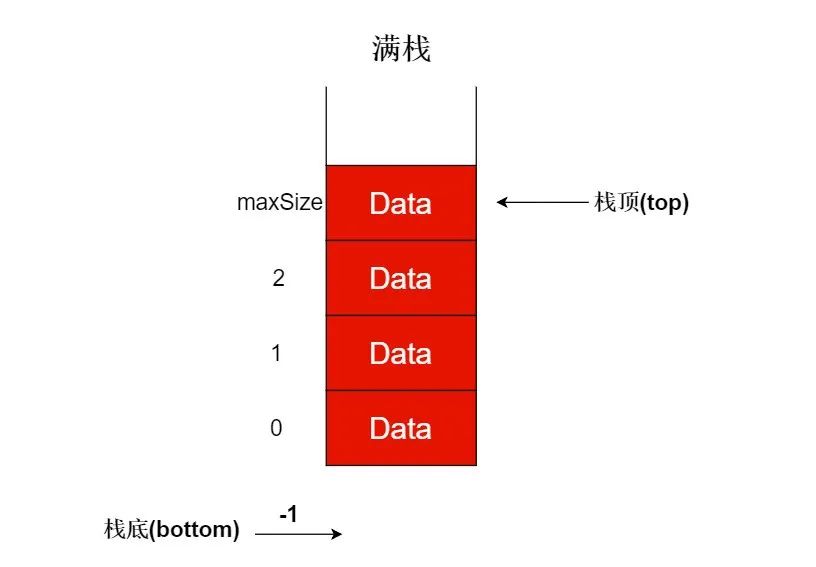
核心代码如下:
@Override
public boolean isFull() {
return top == maxSize - 1;
}
同理,当咱们的bottom==top==-1则表示咱们栈当前没有一个元素,也就是栈为空。
@Override
public boolean isEmpty() {
return bottom == top;
}
2.1.4 入栈
入栈很简单,top向上移动,并且将元素添加到数组即可,如下图所示:
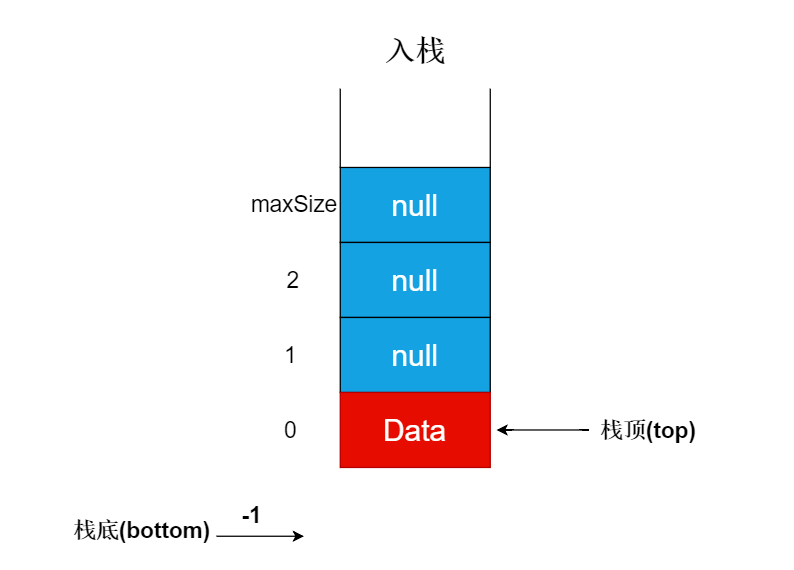
核心代码如下:
@Override
public void push(T element) {
if (isFull()){
throw new RuntimeException("栈已满,无法入栈...");
}
//top上移,并且添加元素
elementData[++top] = element;
//栈内有效结点+1
setSize(getSize() + 1);
}
2.1.5 出栈
出栈和入栈是一个相反的过程,只需将栈顶指针top向下移动即可:
@Override
public T pop() {
if (isEmpty()){
throw new RuntimeException("栈为空,无法出栈...");
}
setSize(getSize() - 1);
return elementData[top--];
}
2.1.6 遍历
@Override
public void show() {
if (isEmpty()){
throw new RuntimeException("栈为空,无法遍历...");
}
System.out.println("栈内存储情况...");
for (int i = top;i > bottom;i--){
System.out.println(elementData[i]);
}
}
2.1.7 测试
package com.ignoarance.stack.test;
import com.ignoarance.stack.ArrayStack;
import com.ignoarance.stack.Stack;
import org.junit.Test;
/**
* @ClassName StackTest
* @Description 栈测试类
* @Author ignorance
* @Version 1.0
**/
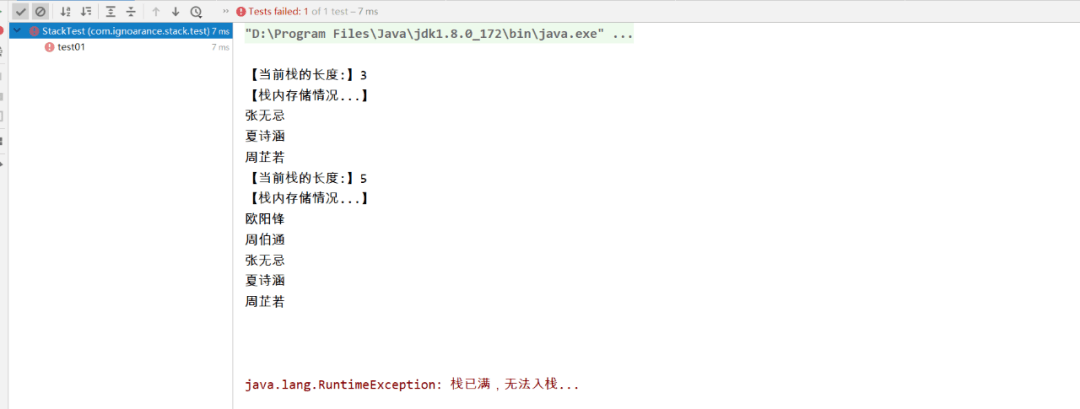
public class StackTest {
@Test
public void test01(){
Stack<String> stack = new ArrayStack<>(new String[5]);
stack.push("周芷若");
stack.push("夏诗涵");
stack.push("张无忌");
stack.push("杨过");
stack.push("郭靖");
stack.pop();
stack.pop();
System.out.println("【当前栈的长度:】" + stack.getSize());
stack.show();
stack.push("周伯通");
stack.push("欧阳锋");
System.out.println("【当前栈的长度:】" + stack.getSize());
stack.show();
stack.push("小龙女");
stack.show();
}
}
2.2链表实现栈
2.2.1 创建结点类
package com.ignoarance.stack.node;
/**
* @ClassName Node
* @Description 结点类
* @Author ignorance
* @Version 1.0
**/
public class Node<T> {
private T item;
public Node<T> next;
public Node(T item) {
this.item = item;
}
@Override
public String toString() {
return "Node{" +
"item=" + item +
'}';
}
}
2.2.2 创建LinkedListStack
在LinkedListStack链表实现栈结构的类中,我们定义bottom和top这两个指针,bottom用于表示栈底,也就是咱们链表的头结点,top用于表示栈顶,也就是咱们链表的尾结点。在构造器中,分别初始化两个指针。
package com.ignoarance.stack;
import com.ignoarance.stack.node.Node;
/**
* @ClassName LinkedListStack
* @Description 链表实现栈
* @Author ignorance
* @Version 1.0
**/
public class LinkedListStack<T> extends Stack<T> {
//栈底指针作为链表的头结点
private Node<T> bottom;
//栈顶指针
private Node<T> top;
public LinkedListStack() {
this.bottom = new Node<>(null);
this.top = null;
}
/**
* 判断当前栈是否满
* 是返回true,否返回false
* @return
*/
@Override
public boolean isFull() {
return false;
}
/**
* 判断当前栈是否空
* 是返回true,否返回false
* @return
*/
@Override
public boolean isEmpty() {
return false;
}
/**
* 入栈核心方法
* @param element
*/
@Override
public void push(T element) {
}
/**
* 出栈方法
* 并返回出栈元素
* @return
*/
@Override
public T pop() {
return null;
}
/**
* 遍历方法
*/
@Override
public void show() {
}
}
2.2.3 判断栈是否为空
@Override
public boolean isEmpty() {
return bottom == null && bottom.next == null;
}
2.2.4 push()方法实现
链表实现栈的先进后出,我们其实可以利用单链表的头插法,前面我们在单链表中的反转中已经介绍过这种方法,相信咱们大家一定不会陌生,以下是思路图:
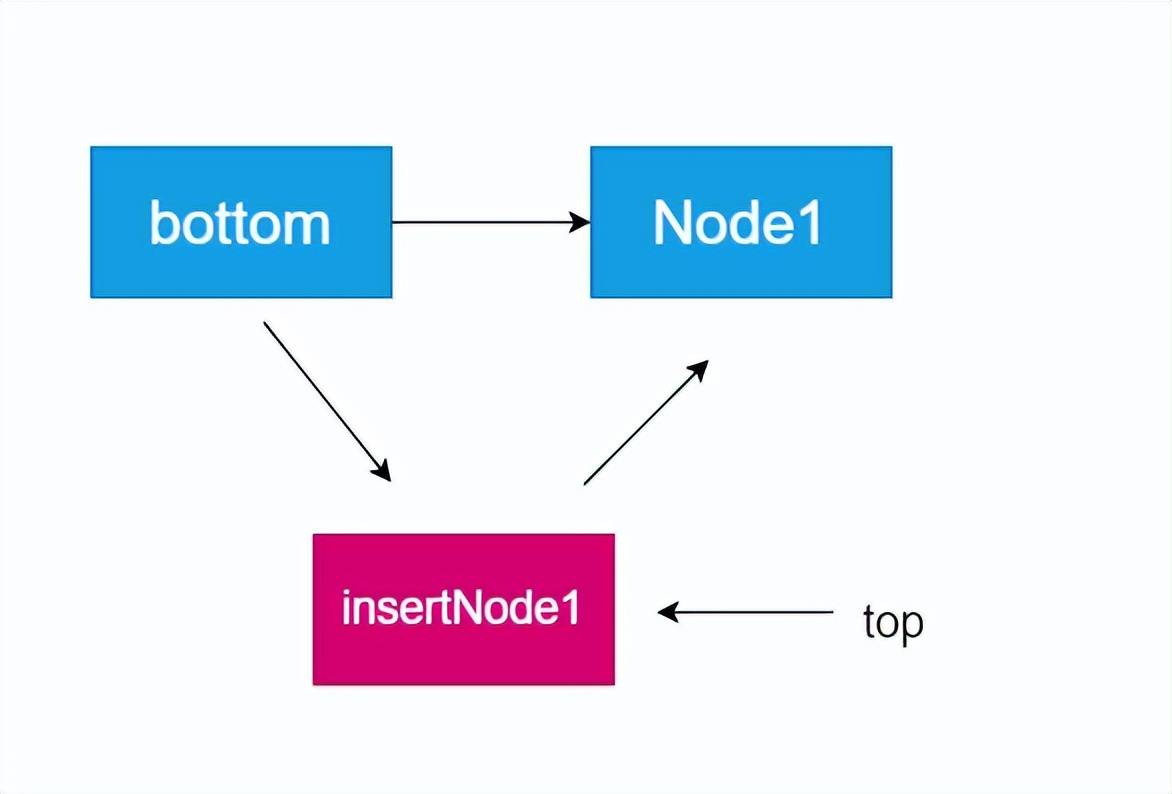
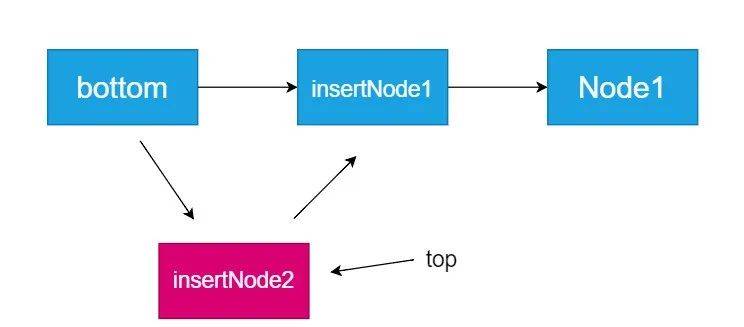
通过头插法,我们每次push的时候,就会将新结点插入到链表最前方,最后pop的时候从第一个开始依次删除就可以。
比如我们加入的顺序是Node->insertNode1->insertNode2,从头开始查找为insertNode2->insertNode1->Node。从而通过头插法巧妙的实现了栈先进先出的思想。代码如下:
@Override
public void push(T element) {
//将数据组装成一个Node结点,因为链表中的最小单位为结点
Node<T> insertNode = new Node<>(element);
//如果节点为空,则加到第一个结点即可
if (isEmpty()){
bottom.next = insertNode;
top = insertNode;
setSize(getSize() + 1);
return;
}
//将新插入结点插入到链表最前端
insertNode.next = top;
bottom.next = insertNode;
top = insertNode;
//有效结点自增
setSize(getSize() + 1);
}
2.2.5 pop()方法实现
知道了链表实现栈思路,那么pop()出栈就显得比较简单了,我们每次pop的时候将链表的第一个结点返回,并将其删除即可,如下图所示:
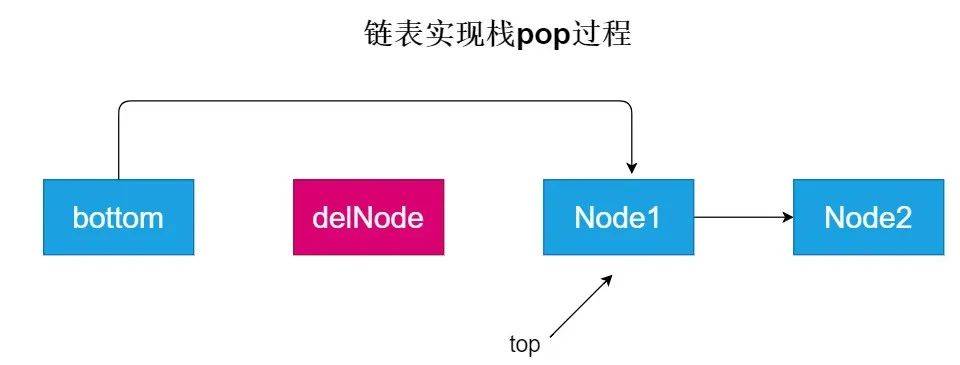
核心代码如下:
@Override
public T pop() {
if (isEmpty()){
throw new RuntimeException("栈为空,无法出栈...");
}
//删除第一个结点
Node<T> popNode = top;
bottom.next = top.next;
top = top.next;
//有效结点自减
setSize(getSize() - 1);
return popNode.getItem();
}
2.2.6 栈的遍历
@Override
public void show() {
if (isEmpty()){
throw new RuntimeException("【栈为空,无法遍历...】");
}
System.out.println("【当前栈的存储情况为:】");
for (Node<T> cur = bottom.next;cur != null;cur = cur.next){
System.out.println(cur);
}
}
2.2.7 测试
@Test
public void test2(){
Stack<String> stack = new LinkedListStack<>();
stack.push("周芷若");
stack.push("夏诗涵");
stack.push("张无忌");
stack.push("杨过");
stack.push("郭靖");
System.out.println("【当前栈的长度:】" + stack.getSize());
stack.show();
stack.pop();
stack.pop();
stack.pop();
stack.pop();
stack.pop();
System.out.println("【当前栈的长度:】" + stack.getSize());
stack.show();
}
三、栈的经典案例
3.1括号匹配问题
力扣上有这么一道题目,给定一个字符串,需要咱们去算这个字符串中的每个"("括号是否成对存在,比如对于字符串"((我们)是)是(程序员)"每个左括号都能找到对应的右括号,说明括号能正确匹配,像"(今天))天)(气真)好"就不满足。
下面需要我们通过代码来实现这个规则,这道题目看起来挺简单,但是在我们去实现时,如果方法选择不恰当,会发现这道题目并不简单。
那么怎么去解决了,这正是咱们栈的一种经典的使用场景。使用其它方式也能实现,但是相比较而言复杂得多。以下是实现思路:
1.创建栈对象,用于存储左括号;
2.遍历字符数组,如果当前字符为左括号,则入栈;
3.如果遍历到的当前字符为右括号,则弹栈,如果弹出的元 素为空, 则表示当前右括号没有与之匹配的左括号。反之则说明当前右括号有匹配的左括号;
4.当循环完字符数组后,我们需要看咱们的栈是否为空,如果为空,说明全部匹配,返回true,反之说明还有多余的右括号,则返回false。
3.1.1 实现代码
package com.ignoarance.stack.test;
import com.ignoarance.stack.LinkedListStack;
import com.ignoarance.stack.Stack;
/**
* @ClassName StackDemo01
* @Description 栈的案例-括号匹配问题
* @Author ignorance
* @Version 1.0
**/
public class StackDemo01 {
public static void mAIn(String[] args) {
String str = "((I am ) a (pretty) b)oy";
System.out.println(isMatch(str));
}
public static boolean isMatch(String resourceStr){
Stack<Character> stack = new LinkedListStack<>();
char[] chars = resourceStr.toCharArray();
for (int i = 0;i < chars.length;i++){
char item = chars[i];
if ('(' == item){
stack.push(item);
continue;
}
if (')' == item){
Character popEle = stack.pop();
if (popEle == null){
return false;
}
}
}
return stack.isEmpty();
}
}
3.1.2 测试(正确情况)
public static void main(String[] args) {
String str = "((I am ) a (pretty) b)oy";
System.out.println(isMatch(str));
}

3.1.3 测试(错误情况)
public static void main(String[] args) {
String str = "(((I am ) a (pretty) b)oy";
System.out.println(isMatch(str));
}
3.2逆波兰表达式完成四则运算
相信计算机专业的同学肯定学过逆波兰表达式,逆波兰表达式是计算机用来进行四则运算的一个表达式,大家都知道咱们数学的四则运算,往往看起来很简单。但是你要是把这个思想告诉计算机,却并不是一件容易的事。
例如对10+(100/4)*5-9进行计算。像我们人脑可以很简单的算出答案,但是如果让你就这个表达式,让你编码让计算机完成呢?是不是就有点头疼了,可不是让你自己分几步做啊,第一步把100/4让计算机算,然后又用这个结果*5。这个问题复杂就复杂在不同的算数符号具有不同的优先级,我们怎么样让计算机知道符号的优先级成为了我们最棘手的问题。
所以呢,为了解决这个问题,就引出了咱们的逆波兰表达式。逆波兰表达式又叫后缀表达式,众所周知,一个运算符对应两个操作数,我们将运算符写在它所作用两个操作数后的一种表达式就是咱们的逆波兰表达式。比如对于a+b,所对应的逆波兰表达式为ab+,对a+(b/c)*d-e,也就是咱们的题目对应的代数式,它所对应的逆波兰表达式为abc/d*+e-。
那么有了逆波兰表达式,我们可以做些什么了,对于刚才那道题目,此时我们就可以使用咱们的栈结构轻松的解决了。实现思路如下:
1.创建栈对象,主要用于存储咱们的操作数;
2.遍历咱们的表达式数组,如果遇到操作数,则入栈;
3.如果遇到运算符,则从栈中弹出两个操作数,并且计算结果,将最后的结果重新入栈。
4.按照第3步的逻辑,当咱们的表达式数组遍历完成以后,此时栈中会存在一个元素,这个元素就是咱们最后的元素结果,将其出栈即可。
3.2.1 实现代码
package com.ignoarance.stack.test;
import com.ignoarance.stack.LinkedListStack;
import com.ignoarance.stack.Stack;
/**
* @ClassName StackDemo02
* @Description 栈应用案例-逆波兰表达式实现四则运算
* @Author ignorance
* @Version 1.0
**/
public class StackDemo02 {
public static void main(String[] args) {
String[] express = {"10","100","4","/","5","*","+","9","-"};
System.out.println(compute(express));
}
public static Integer compute(String[] expressArray){
String sign = "+-*/";
Stack<Integer> stack = new LinkedListStack<>();
for (String item : expressArray){
if (sign.contains(item)){
Integer num1 = stack.pop();
Integer num2 = stack.pop();
stack.push(oper(num1,num2,item));
continue;
}
stack.push(Integer.parseInt(item));
}
return stack.pop();
}
private static Integer oper(Integer num1,Integer num2,String oper){
switch (oper){
case "+" : return num2 + num1;
case "-" : return num2 - num1;
case "*" : return num2 * num1;
case "/" : return num2 / num1;
default:throw new RuntimeException("不支持的操作类型...");
}
}
}
3.2.2 测试

四、综合代码
4.1Stack抽象父类
package com.ignoarance.stack;
/**
* @ClassName Stack
* @Description 栈的父类
* @Author ignorance
* @Version 1.0
**/
public abstract class Stack<T> {
private int size;//栈的实际有效元素个数
public int getSize() {
return size;
}
public void setSize(int size) {
this.size = size;
}
/**
* 判断当前栈是否满
* 是返回true,否返回false
* @return
*/
public abstract boolean isFull();
/**
* 判断当前栈是否空
* 是返回true,否返回false
* @return
*/
public abstract boolean isEmpty();
/**
* 入栈核心方法
*/
public abstract void push(T element);
/**
* 出栈方法
* 并返回出栈元素
* @return
*/
public abstract T pop();
/**
* 遍历方法
*/
public abstract void show();
}
4.2ArrayStack
package com.ignoarance.stack;
import java.util.Arrays;
/**
* @ClassName ArrayStack
* @Description 数组实现栈核心类
* @Author ignorance
* @Version 1.0
**/
public class ArrayStack<T> extends Stack<T> {
private T[] elementData;//栈的核心存储结构【数组】
private final int maxSize;//数组最大长度
private int bottom;//栈底指针
private int top;//栈顶指针
public ArrayStack(T[] elementData) {
this.elementData = elementData;//初始化底层数组
this.maxSize = elementData.length;
this.bottom = -1;//将栈底索引置为-1
this.top = -1;//将栈顶索引置为-1
}
@Override
public boolean isFull() {
return top == maxSize - 1;
}
@Override
public boolean isEmpty() {
return bottom == top;
}
@Override
public void push(T element) {
if (isFull()){
throw new RuntimeException("栈已满,无法入栈...");
}
//top上移,并且添加元素
elementData[++top] = element;
//栈内有效结点+1
setSize(getSize() + 1);
}
@Override
public T pop() {
if (isEmpty()){
throw new RuntimeException("栈为空,无法出栈...");
}
setSize(getSize() - 1);
return elementData[top--];
}
@Override
public void show() {
if (isEmpty()){
throw new RuntimeException("栈为空,无法遍历...");
}
System.out.println("【栈内存储情况...】");
for (int i = top;i > bottom;i--){
System.out.println(elementData[i]);
}
}
}
4.3结点类Node
package com.ignoarance.stack.node;
/**
* @ClassName Node
* @Description 结点类
* @Author ignorance
* @Version 1.0
**/
public class Node<T> {
private T item;
public Node<T> next;
public Node(T item) {
this.item = item;
}
public T getItem() {
return item;
}
public void setItem(T item) {
this.item = item;
}
@Override
public String toString() {
return "Node{" +
"item=" + item +
'}';
}
}
4.4LinkedListStack
package com.ignoarance.stack;
import com.ignoarance.stack.node.Node;
/**
* @ClassName LinkedListStack
* @Description 链表实现栈
* @Author ignorance
* @Version 1.0
**/
public class LinkedListStack<T> extends Stack<T> {
//栈底指针作为链表的头结点
private Node<T> bottom;
//栈顶指针
private Node<T> top;
public LinkedListStack() {
this.bottom = new Node<>(null);
this.top = null;
}
/**
* 判断当前栈是否满,也就是链表是否有结点
* 是返回true,否返回false
* @return
*/
@Override
public boolean isFull() {
throw new RuntimeException("不支持的操作...");
}
/**
* 判断当前栈是否空
* 是返回true,否返回false
* @return
*/
@Override
public boolean isEmpty() {
return bottom == null || bottom.next == null;
}
/**
* 入栈核心方法
* @param element
*/
@Override
public void push(T element) {
//将数据组装成一个Node结点,因为链表中的最小单位为结点
Node<T> insertNode = new Node<>(element);
//如果节点为空,则加到第一个结点即可
if (isEmpty()){
bottom.next = insertNode;
top = insertNode;
setSize(getSize() + 1);
return;
}
//将新插入结点插入到链表最前端
insertNode.next = top;
bottom.next = insertNode;
top = insertNode;
//有效结点自增
setSize(getSize() + 1);
}
/**
* 出栈方法
* 并返回出栈元素
* @return
*/
@Override
public T pop() {
if (isEmpty()){
throw new RuntimeException("栈为空,无法出栈...");
}
//删除第一个结点
Node<T> popNode = top;
bottom.next = top.next;
top = top.next;
//有效结点自减
setSize(getSize() - 1);
return popNode.getItem();
}
/**
* 遍历方法
*/
@Override
public void show() {
if (isEmpty()){
throw new RuntimeException("【栈为空,无法遍历...】");
}
System.out.println("【当前栈的存储情况为:】");
for (Node<T> cur = bottom.next;cur != null;cur = cur.next){
System.out.println(cur);
}
}
}
4.5Stack测试类
package com.ignoarance.stack.test;
import com.ignoarance.stack.ArrayStack;
import com.ignoarance.stack.LinkedListStack;
import com.ignoarance.stack.Stack;
import org.junit.Test;
/**
* @ClassName StackTest
* @Description 栈测试类
* @Author ignorance
* @Version 1.0
**/
public class StackTest {
@Test
public void test01(){
Stack<String> stack = new ArrayStack<>(new String[5]);
stack.push("周芷若");
stack.push("夏诗涵");
stack.push("张无忌");
stack.push("杨过");
stack.push("郭靖");
stack.pop();
stack.pop();
System.out.println("【当前栈的长度:】" + stack.getSize());
stack.show();
stack.push("周伯通");
stack.push("欧阳锋");
System.out.println("【当前栈的长度:】" + stack.getSize());
stack.show();
stack.push("小龙女");
stack.show();
}
@Test
public void test2(){
Stack<String> stack = new LinkedListStack<>();
stack.push("周芷若");
stack.push("夏诗涵");
stack.push("张无忌");
stack.push("杨过");
stack.push("郭靖");
System.out.println("【当前栈的长度:】" + stack.getSize());
stack.show();
stack.pop();
stack.pop();
stack.pop();
stack.pop();
stack.pop();
System.out.println("【当前栈的长度:】" + stack.getSize());
stack.show();
}
}
4.6Stack案例一
package com.ignoarance.stack.test;
import com.ignoarance.stack.LinkedListStack;
import com.ignoarance.stack.Stack;
/**
* @ClassName StackDemo01
* @Description 栈的案例-括号匹配问题
* @Author ignorance
* @Version 1.0
**/
public class StackDemo01 {
public static void main(String[] args) {
String str = "(((I am ) a (pretty) b)oy";
System.out.println(isMatch(str));
}
public static boolean isMatch(String resourceStr){
Stack<Character> stack = new LinkedListStack<>();
char[] chars = resourceStr.toCharArray();
for (int i = 0;i < chars.length;i++){
char item = chars[i];
if ('(' == item){
stack.push(item);
continue;
}
if (')' == item){
Character popEle = stack.pop();
if (popEle == null){
return false;
}
}
}
return stack.isEmpty();
}
}
4.7Stack案例二
package com.ignoarance.stack.test;
import com.ignoarance.stack.LinkedListStack;
import com.ignoarance.stack.Stack;
/**
* @ClassName StackDemo02
* @Description 栈应用案例-逆波兰表达式实现四则运算
* @Author ignorance
* @Version 1.0
**/
public class StackDemo02 {
public static void main(String[] args) {
String[] express = {"10","100","4","/","5","*","+","9","-"};
System.out.println(compute(express));
}
public static Integer compute(String[] expressArray){
String sign = "+-*/";
Stack<Integer> stack = new LinkedListStack<>();
for (String item : expressArray){
if (sign.contains(item)){
Integer num1 = stack.pop();
Integer num2 = stack.pop();
stack.push(oper(num1,num2,item));
continue;
}
stack.push(Integer.parseInt(item));
}
return stack.pop();
}
private static Integer oper(Integer num1,Integer num2,String oper){
switch (oper){
case "+" : return num2 + num1;
case "-" : return num2 - num1;
case "*" : return num2 * num1;
case "/" : return num2 / num1;
default:throw new RuntimeException("不支持的操作类型...");
}
}
}
总结
在本篇文章中,咱们主要讲了栈这种特殊的数据结构,也是咱们特别常见的数据结构。对栈结构又通过数组和链表两种方式进行实现,代码并不算难。重点值得关注的是栈结构的核心思想,对我们来说能够理解是特别重要的。像咱们通过栈完成了两个案例,希望能够帮助大家对其思想有更深的了解和认识。
我们在不断学习的过程,会发现编程是一件特别具有挑战性的事情,有时候咱们学得越多,总会发现自己不会的也越多,当咱们真正理解了设计者为我们提供的思想,又会突然间豁然开朗,不由对他们的智慧心生敬仰。
所以呢,在学习的路途中,有无数的同道者一起都在前行,努力的人不会一直孤独的,总有一天我们也会因为不断的努力,不论是技术还是生活,都会发生美好的改变。所以,加油吧!