
逻辑回归(Logistic Regression)是一种广义的线性回归分析模型,常用于数据挖掘、疾病自动诊断、经济预测等领域。它根据给定的自变量数据集来估计事件的发生概率。变量的范围在0和1之间,通常用于二分类问题,最终输出的预测是一个非线性的S型函数,称为logistic function, g()。
逻辑递归(Recursive Logic)是一种在逻辑学中使用的推理方法,它基于递归定义和递归推理规则,用于描述和推导关于递归结构的命题。用于研究自指的悖论和不完全性定理。它是基于自我引用和递归定义的思想,将逻辑和计算理论相结合,形成了一种强有力的推理工具。
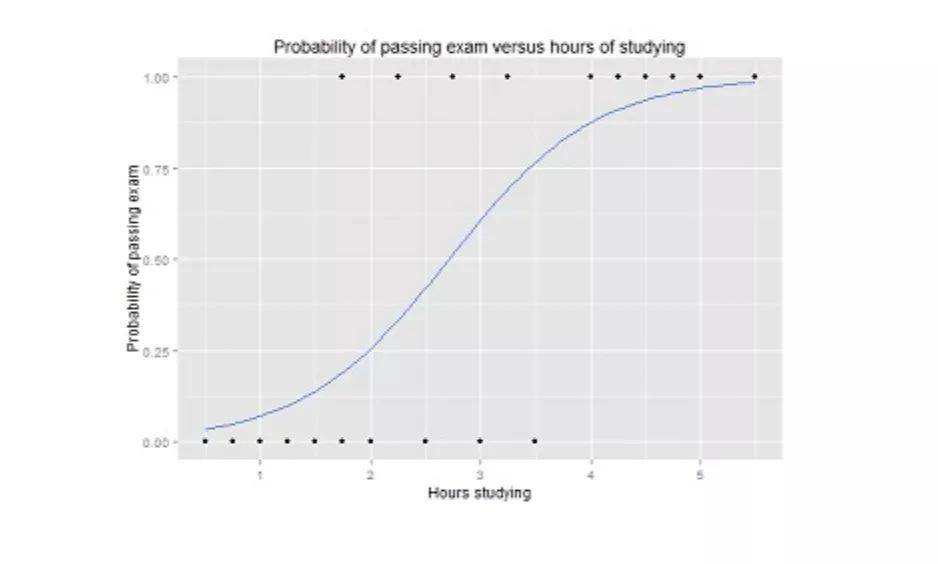
例如,下图为逻辑回归曲线图,显示了考试通过概率与学习时间的关系。
再如,在探讨引发疾病的危险因素时,可以根据危险因素预测疾病发生的概率。选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群必定具有不同的体征与生活方式等。通过逻辑回归分析,可以得到自变量的权重,从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。
需要注意的是,逻辑递归的推理过程可能面临一些挑战,如悖论和无限循环等。因此,在使用逻辑递归进行推理时,需要注意对递归定义和推理规则的合理限制,以避免逻辑矛盾和无穷循环的问题。
逻辑递归在逻辑学和计算理论中有广泛的应用。它被用于形式系统的研究,证明理论中的定理和推理规则,以及计算机科学中的递归算法和程序设计等领域。