详解程序员必学的十大算法

作为一名程序员，掌握各种算法可以帮助我们解决各种复杂的问题，提高代码的效率和性能，同时也是面试中常被考察的重要内容之一。无论是开发新的软件应用、优化现有的算法逻辑还是解决各类计算问题，算法都是不可或缺的工具。因此，程序员掌握一系列常用的算法，以确保能够高效地编写出稳定、功能强大的软件。

常用的算法类别及其应用如下：

一. 排序算法

1.冒泡排序：用于将一组数据按照升序或降序进行排列，它通过比较相邻元素的大小来进行交换，直到整个序列排序完成。

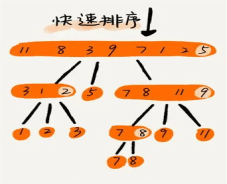
2.快速排序：快速排序是一种常用且高效的排序算法，它采用递归的方式将问题划分为更小的子问题，并使用一个基准元素进行排序。

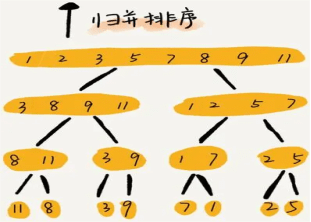
3.归并排序：归并排序采用分治策略，将问题逐步细化并通过合并操作得到最终的有序结果。

二. 搜索算法

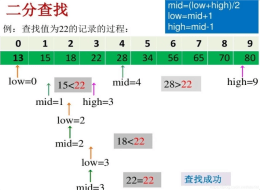
1.二分查找：二分查找适用于有序数组，它将目标值与数组的中间元素进行比较，从而缩小搜索范围，直到找到目标元素或确定不存在。

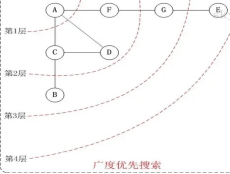
2.广度优先搜索：广度优先搜索用于遍历或搜索图或树的结构。它按照层次的顺序遍历节点，先访问根节点，然后是所有与根节点相邻的节点，然后是他们的邻节点，依次类推。

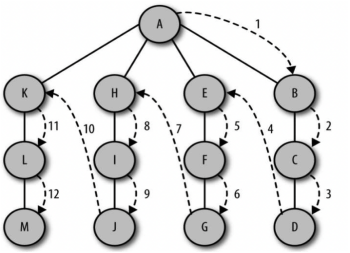
3.深度优先搜索：深度优先搜索也用于遍历或搜索图或树的结构。它从根节点开始，沿着一条路径搜索到最深的节点，然后再回溯到之前的节点继续搜索。

三. 图算法

1.最短路径算法：最短路径算法用于寻找两个节点之间的最短路径。常用的最短路径算法有Dijkstra算法和Floyd-Warshall算法。

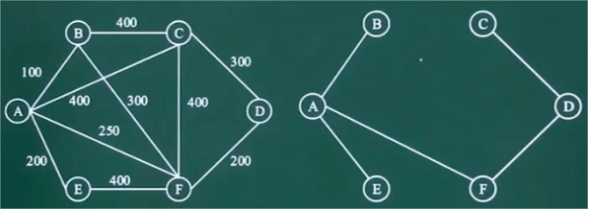
2.最小生成树算法：最小生成树算法用于在一个带权重的无向图中找出一棵包含所有节点的子树，并且使得该子树的边权重之和最小。常见的最小生成树算法有Prim算法和Kruskal算法。

四.动态规划

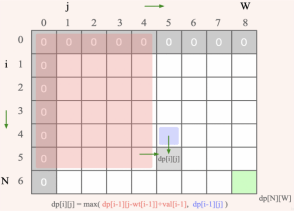
1.背包问题：背包问题是一类经典的优化问题，其中给定一组物品和一个背包容量，目标是将物品放入背包中，使得物品总价值最大化，同时不超过背包的容量。

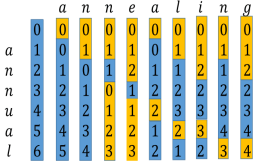
2.最长公共子序列：最长公共子序列问题是一类经典的字符串处理问题，目标是找出两个字符串中最长的共同子序列的长度。